Journal of Radiology and Imaging
An International Peer-Reviewed Open Access Journal
ISSN 2399-8172


- Download PDF
- |
- Download Citation
- |
- Email a Colleague
- |
- Share:
-
- Tweet
-

Journal of Radiology and Imaging
Volume 2, Issue 3, March 2017, Pages 14–35
Original researchOpen Access
10-MV X-ray dose calculation in water for MLC and wedge fields using a convolution method with X-ray spectra reconstructed as a function of off-axis distance
-
Akira Iwasaki1,*
 ,
Shigenobu Kimura2,
Kohji Sutoh2,
Kazuo Kamimura2,
Makoto Sasamori3,
Morio Seino4,
Fumio Komai4,
Masafumi Takagi5,
Shingo Terashima6,
Yoichiro Hosokawa6,
Hidetoshi Saitoh7 and
Masanori Miyazawa8
,
Shigenobu Kimura2,
Kohji Sutoh2,
Kazuo Kamimura2,
Makoto Sasamori3,
Morio Seino4,
Fumio Komai4,
Masafumi Takagi5,
Shingo Terashima6,
Yoichiro Hosokawa6,
Hidetoshi Saitoh7 and
Masanori Miyazawa8
- 1 2-3-24 Shimizu, Hirosaki, Aomori 036-8254, Japan
- 2 Department of Radiology, Aomori City Hospital, 1-14-20 Katta, Aomori 030-0821, Japan
- 3 Department of Radiology, Misawa City Hospital, 4-1-10 Chuo-cho, Misawa, Aomori 033-0051, Japan
- 4 Department of Radiology, Hirosaki University Hospital, 53 Hon-cho, Hirosaki, Aomori 036-8563, Japan
- 5 Department of Radiology, Hirosaki Chuo Hospital, 3-1 Yoshino-cho, Hirosaki, Aomori 036-8188, Japan
- 6 Graduate School of Health Sciences, Hirosaki University, 66-1 Hon-cho, Hirosaki, Aomori 036-8564, Japan
- 7 Graduate School of Human Health Sciences, Tokyo Metropolitan University, 7-2-10 Higashi-Ogu, Arakawa-ku, Tokyo, 116-8551, Japan
- 8 Technology of Radiotherapy Corporation, 2-1-2 Koishikawa, Bunkyo-ku, Tokyo, 175-0092, Japan
*Corresponding author: Akira Iwasaki, 2-3-24 Shimizu, Hirosaki, Aomori 036-8254, Japan. Tel.: +172-33-2480; E-mail: fmcch384@ybb.ne.jp
Received 28 November 2016 Revised 9 February 2017 Accepted 25 February 2017 Published 10 March 2017
DOI: http://dx.doi.org/10.14312/2399-8172.2017-4
Copyright: © 2017 Iwasaki A, et al. Published by NobleResearch Publishers. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
AbstractTop
Purposes: This paper highlights a 10-MV X-ray convolution dose calculation method in water using primary and scatter dose kernels formed for energy bins of X-ray spectra reconstructed as a function of the off-axis distance for a linear accelerator equipped with pairs of upper and lower jaws, a multileaf collimator (MLC) and a wedge filter. Methods: The reconstructed X-ray spectra set was composed of 11 energy bins. To estimate the in-air beam intensities at points on the isocenter plane for an MLC field, we employed an MLC leaf-field output subtraction method, using an extended radiation source on each of the X-ray target and the flattening filter as well as simplified two-dimensional plates to simulate the three-dimensional jaws and MLC structures. A special correction factor was introduced for nonuniform incident beam intensities, particularly produced at MLC fields. The in-phantom dose calculation was performed by treating the phantom, the wedge filter, the wedge holder and the MLC as parts of a unified irradiated body, where we proposed to use a special factor for the density scaling theorem within the unified irradiated body. Conclusions: The phantom dose was generally separated into nine dose-components: The primary and scatter dose-components produced in the phantom; the primary and scatter dose-components emanating from the wedge, the wedge holder and the MLC; and the electron contamination dose-component. From the calculated and measured percentage depth dose (PDD) and off-center ratio (OCR) datasets, we may conclude that the convolution method can achieve accurate dose calculations even under MLC and/or wedge filtration.
Keywords: convolution method; X-ray spectra; dose kernels; wedge; multileaf collimation; MLC leaf-field output subtraction
Research highlightsTop
Convolution methods are convenient for three-dimensional (3D) dose calculations, especially for an irregular-beam field with a non-uniform incident-beam intensity distribution. For a convolution method, we performed theoretical and experimental studies on 10-MV X-ray dose calculations in water phantoms with multileaf collimation (MLC) and/or wedge filtration using a linear accelerator equipped with a pair of upper jaws, a pair of lower jaws, an MLC and a wedge filter. The in-phantom dose calculation was performed by treating the phantom, the wedge filter, the wedge holder and the MLC as parts of a unified irradiated body. We can conclude that the convolution method can achieve accurate dose calculations even under MLC and/or wedge filtration.
IntroductionTop
Megavoltage X-ray beams from linear accelerators are used for radiation therapy. The X-ray radiation produced in the X-ray target pass through a flattening filter that is symmetric with respect to the isocenter axis. The flattening filter makes the beam intensity distribution relatively uniform across the field. The filter is thickest in the middle and tapers off toward the edges; therefore, the X-ray spectrum is a function of the off-axis distance (radiation softening becomes more pronounced with increasing off-axis distance).
The dose at a point in a medium irradiated by an X-ray beam can be separated into three components. One is the primary dose, arising directly from primary photons that have not interacted with the medium before reaching the point. Another is the dose from scattered radiation originating from all points hit by primary photons in the medium. The last is the contamination dose, caused by electrons from the treatment head and air volume. With model-based algorithms, one can calculate the primary, scatter and contamination dose components separately. Convolution (or superposition) methods are in the class of model-based algorithms. They are convenient for three-dimensional (3D) dose calculations, especially for an irregular-beam field with a nonuniform incident-beam intensity distribution. As reviewed by Ahnesjö and Aspradakis [1], there are two kinds of convolution methods: one is a method that uses pencil-beam kernels, and the other is a method that uses point-dose kernels.
With respect to the latter convolution method, its numerical convolution is also called “the collapsed cone convolution” [2]. The present paper deals with a kind of collapsed cone convolution; however, it is to be emphasized that the dose calculation is performed using multiple primary- and scatter-dose kernels that are formed with the use of X-ray spectra reconstructed [3, 4] as a function of the off-axis distance.
For accurate primary and scatter dose calculations using convolution methods, Iwasaki [5] stipulated that the following four irradiation conditions be met: (a) a nondivergent beam, (b) a homogeneous phantom, (c) a beam attenuation coefficient along ray lines that is not a function of the depth and off-axis distance, and (d) an incident beam intensity that is uniform within the irradiation field and zero outside it. We have not yet dealt with the condition described in (a). Iwasaki, et al. [6] and Kimura, et al. [7] dealt with the condition described in (b) using inhomogeneous phantoms, proposing a correction factor for calculation of the primary dose within thorax-like phantoms, and also dealt with the condition described in (c) using X-ray spectra reconstructed as a function of the off-axis distance. In the present paper, we proposed a special correction factor for nonuniformity of the incident beam intensity described in the above (d) using multileaf collimator (MLC) and/or wedge fields. Because the MLC and wedge devices are usually made of high-Z materials, they can induce large changes in the incident beam intensity (also including the X-ray spectrum changes). The dose calculation simulations are performed using 10-MV X-ray beams, focusing on percentage depth dose (PDD) and off-center ratio (OCR) datasets in water phantoms.
Materials and methodsTop
The physical parameters of the materials used in this study were evaluated using data tables published by Hubbell [8]. We used 10-MV X-ray beams from a linear accelerator (CL-2100C; Varian Medical Systems, Palo Alto, CA, USA). The treatment head contains pairs of upper and lower jaws: upper-1, -2 and lower-1, -2 (tungsten alloy) as the jaw collimator which is able to form a jaw field ≤ 40 × 40 cm2 on the isocenter plane 100 cm distant from the source (S) (or the X-ray target). The treatment head also features an MLC (Millennium 120 Leaf; Varian Medical Systems) under the jaw-collimator device. Each leaf moves in the same direction as the lower jaws. We used wedge filters supplied by the manufacturer that are designed to be installed directly on the treatment head. The wedge filters, made of steel or lead alloys, form isodose angles of 15°, 30°, 45° and 60° in water and are mounted on an acrylic plate (wedge holder). Figure 1 diagrams the treatment head with an installed wedge. We let Ajaw and AMLC denote the jaw and MLC fields, respectively, measured on the isocenter plane.
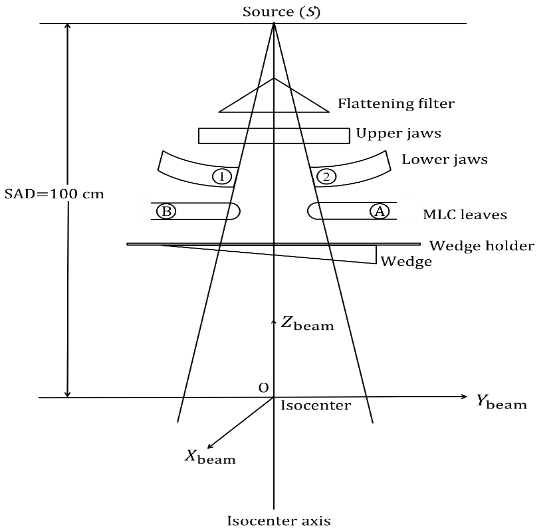
Symbols and units
We use the following symbols and units in this paper: the spectra-related energies (EN and ΔEN) are expressed in MeV; the normalized set of reconstructed energy fluences (Ψ's) is expressed in MeV-1; the total in-air beam energy fluence ![]() is expressed in J/cm2; the linear attenuation coefficients (e.g., μwater, μphan, μwedge, μMLC,
is expressed in J/cm2; the linear attenuation coefficients (e.g., μwater, μphan, μwedge, μMLC, ![]() ) for media are expressed in cm-1); the lengths (Ξ, Η, ξ, η, R, r, R0, etc.) are expressed in cm; the position vectors (
) for media are expressed in cm-1); the lengths (Ξ, Η, ξ, η, R, r, R0, etc.) are expressed in cm; the position vectors (![]() ) are expressed in cm; the primary and scatter dose components
) are expressed in cm; the primary and scatter dose components ![]() are expressed in Gy; the beam water collision kerma (or the primary water collision kerma) components
are expressed in Gy; the beam water collision kerma (or the primary water collision kerma) components ![]() are expressed in Gy; the dose kernels (H1,2, K1,2, hphan, hwedge, hMLC, kphan, kwedge, kMLC, etc.) are expressed in cm-3; the volume element (ΔV) is expressed in cm3; and the area element (ΔS) is expressed in cm2.
are expressed in Gy; the dose kernels (H1,2, K1,2, hphan, hwedge, hMLC, kphan, kwedge, kMLC, etc.) are expressed in cm-3; the volume element (ΔV) is expressed in cm3; and the area element (ΔS) is expressed in cm2.
Theoretical studies We tried to calculate the dose at a point generally in an inhomogeneous phantom by treating the phantom, the wedge filter, the wedge holder and the MLC as parts of a unified irradiated body. For this calculation model, we used an orthogonal coordinate system of (Xbeam, Ybeam, Zbeam) (Figures 1 and 2), setting the origin (O) at the isocenter. We denote the Zbeam axis as the line connecting the source (S) and the origin (O), coinciding with the isocenter axis, and assume that the Xbeam and Ybeam axes perpendicularly intersect the upper- and lower-jaw field edges, respectively, on the isocenter plane (Zbeam = 0 cm), calling this the “beam coordinate system”. The MLC leaves move parallel to the Ybeam axis, in the same direction as that of the lower jaws. To calculate the expressions of equations 1−3 described in the following text to evaluate the dose at a point P(Xc, Yc, Zc) in the phantom (Figure 2), we use two other coordinate systems in addition to the beam coordinate system (Xbeam, Ybeam, Zbeam): one is the orthogonal coordinate system (xv, yv, zv) with the origin at point P (it should be noted that the (xv, yv, zv) coordinate system just coincides with the (Xbeam, Ybeam, Zbeam) coordinate system when point P coincides with the isocenter (O); and the other is the polar coordinate system (r', Φ, θ) directly associated with the (xv, yv, zv) coordinate system.

Dose calculation principle
The dose calculation was performed using a convolution method that utilizes special types of in-water primary and scatter dose kernels (H1,2 and K1,2 (see Appendix A)), formed for the energy bins of X-ray spectra [3, 4] reconstructed as a function of the off-axis distance. It should be noted that the usual number of energy bins is approximately ten, and that the reconstructed X-ray spectra can reasonably be applied [4] to media with a wide range of effective Z numbers (e.g., from water to lead). When applying the density scaling theorem [9-11] to the in-water primary and scatter dose kernels again under the conditions that the phantom, wedge filter, wedge holder and MLC are treated as parts of a unified irradiated body, the use of the relative electron density (ρe) is not feasible. This is because the effective Z numbers of the media within the unified irradiated body are quite different from one another, depending on the energy bins of the reconstructed X-ray spectra. Thus, we propose to use a factor of μmed/ μwater (the relative attenuation factor) for the medium of each volume element within the unified irradiated body, where μmed and μwater are the linear attenuation coefficients of the volume element material and water, respectively, and are determined by each of the energy bins of the reconstructed X-ray spectra. For the volume elements existing along a line connecting two points, we propose to use the mean relative attenuation factor, ![]() instead of using the mean relative electron density
instead of using the mean relative electron density ![]() . It should be noted that the linear attenuation coefficients μmed, μwater and
. It should be noted that the linear attenuation coefficients μmed, μwater and ![]() generally change with the energy bin of the reconstructed X-ray spectra, whereas ρe or
generally change with the energy bin of the reconstructed X-ray spectra, whereas ρe or ![]() does not. In addition, for water-like media, we can assume ρe = μmed/ μwater and
does not. In addition, for water-like media, we can assume ρe = μmed/ μwater and ![]() for any energy bin. This method of using the linear attenuation coefficients may be effective for handling the scatter dose kernels. However, it may not be effective for handling the primary dose kernels because the primary dose is caused by the secondary electrons generated by the interaction between the volume element and the primary photons. The secondary electrons do not have a strong relationship with photon attenuation from the standpoint of energy deposition in media.
for any energy bin. This method of using the linear attenuation coefficients may be effective for handling the scatter dose kernels. However, it may not be effective for handling the primary dose kernels because the primary dose is caused by the secondary electrons generated by the interaction between the volume element and the primary photons. The secondary electrons do not have a strong relationship with photon attenuation from the standpoint of energy deposition in media.
Figure 2 also shows a quadrangular pyramid in polar coordinates, whose apex is situated at point P. It shows how to calculate the primary, scatter and electron contamination doses delivered to point P, where the primary and scatter doses arise from the volume elements (ΔV’s) in the unified irradiated body; and the electron contamination dose arises from the area element ΔS. Regarding to the volume elements (ΔV's) and area elements (ΔS's), we employed a series of θ, Δθ, Φ, ΔΦ, r' data (see Appendix B). For the convolution dose calculation, (a) we used a set of X-ray spectra reconstructed as a function of the off-axis distance, letting the bin energies be EN (N = 1, 2,....., Nmax with Nmax ≅ 10) for each off-axis distance; (b) we used primary dose kernels (hphan, hwedge, hw_hold and hMLC) and scatter dose kernels (kphan, kwedge, kw_hold and kMLC) as a function of EN for the volume and area elements, where these dose kernels are rebuilt from the in-water primary and scatter dose kernels (H1,2 and K1,2); and (c) we estimated values of ![]() as a function of EN for each of the volume and area elements.
as a function of EN for each of the volume and area elements.
For dose calculation generally under the presence of the MLC and a wedge filter, we divided the dose to point P into nine components: (a) the primary and scatter doses ![]() produced in the phantom; (b) the primary and scatter doses
produced in the phantom; (b) the primary and scatter doses ![]() emanating from the wedge filter; (c) the primary and scatter doses
emanating from the wedge filter; (c) the primary and scatter doses ![]() emanating from the wedge holder; (d) the primary and scatter doses
emanating from the wedge holder; (d) the primary and scatter doses ![]() emanating from the MLC; and (e) the contamination dose Dcont caused by the electrons emanating from the treatment head and the air volume.
emanating from the MLC; and (e) the contamination dose Dcont caused by the electrons emanating from the treatment head and the air volume.
It should be noted that this calculation method does not strictly take into account the primary and scatter doses due to the secondary electrons and scattered photons, respectively, produced in the upper and lower jaws. Instead, it treats the radiation reflected from the jaws as a small increase in the in-air beam intensity using a jaw radiation reflection factor [6] that lies outside the jaw field, as described by a Monte Carlo simulation model [12] stating that the photons scattered from the jaws can be ignored when estimating the in-air beam intensity within the jaw field.
Within the unified irradiated body, we set the beam water collision kerma ![]() to act on the dose kernel at each ΔV or ΔS element point. When the beam water collision kerma should be determined based on the open jaw field without the MLC device, we denote it as
to act on the dose kernel at each ΔV or ΔS element point. When the beam water collision kerma should be determined based on the open jaw field without the MLC device, we denote it as ![]() . When the beam water collision kerma should be determined based on the open MLC field under a given jaw field, we denote it as
. When the beam water collision kerma should be determined based on the open MLC field under a given jaw field, we denote it as ![]() .
.
Next, we describe the dose calculation approaches using position vectors, generally taking an irradiation case in which both wedge and MLC devices are installed in a jaw field (Figure 2a). We let Lc denote the position vector to a dose calculation point P, drawn from the source (S); and ![]() denote the position vectors to volume elements ΔV's in the phantom, wedge filter, wedge holder and MLC, respectively, drawn from the source (S); and LΔs denote the position vector to an area element (ΔS) on the phantom surface, drawn from the source (S). Then the primary, scatter and electron contamination dose calculations are performed using the follow approaches.
denote the position vectors to volume elements ΔV's in the phantom, wedge filter, wedge holder and MLC, respectively, drawn from the source (S); and LΔs denote the position vector to an area element (ΔS) on the phantom surface, drawn from the source (S). Then the primary, scatter and electron contamination dose calculations are performed using the follow approaches.
(a) The primary dose calculation approach:
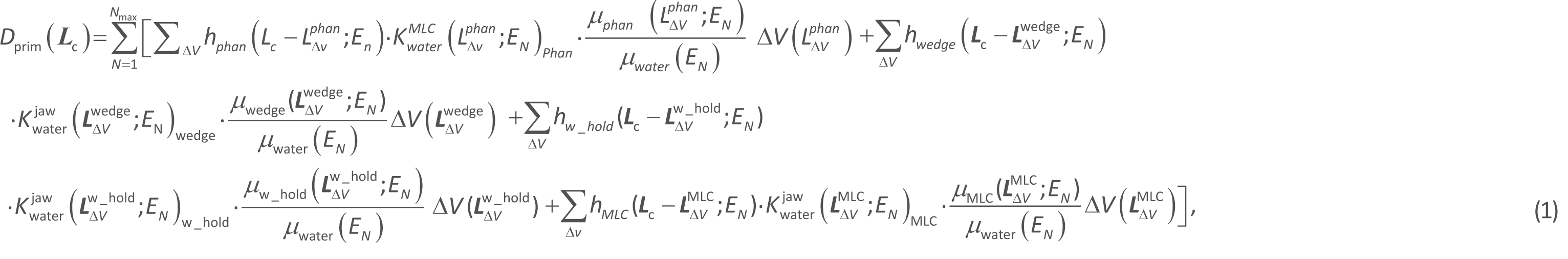
where ![]() express the beam water collision kermas at the corresponding volume elements (ΔV’s), respectively, in the phantom and in the wedge or MLC device (equations 40-42, 46).
express the beam water collision kermas at the corresponding volume elements (ΔV’s), respectively, in the phantom and in the wedge or MLC device (equations 40-42, 46).
(b) The scatter dose calculation approach:
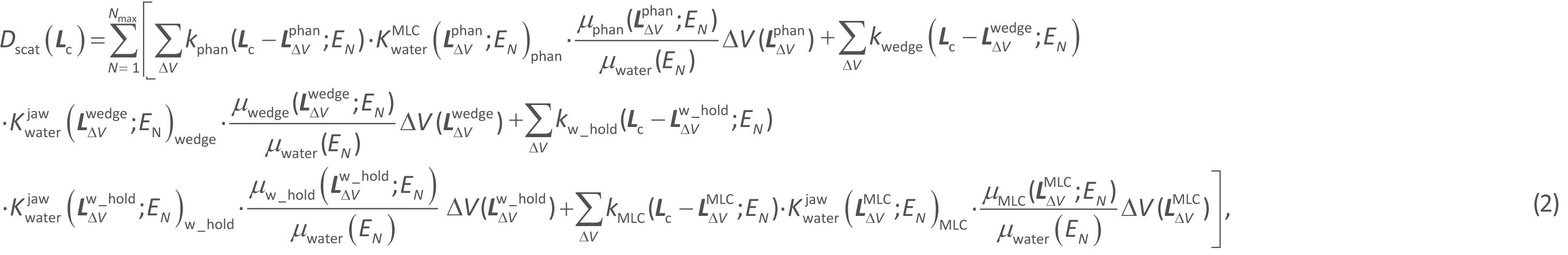
(c) The contamination dose calculation approach:
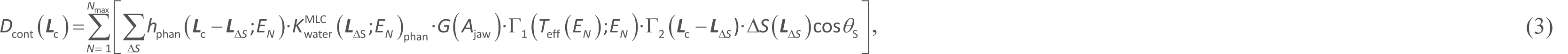
where ![]() express the beam water collision kerma at the corresponding phantom surface element (ΔS) (equation 43); ΔS is defined as the size of the area element on the phantom surface, which faces the source (S) without interception by the phantom; θS is the angle between the normal vector line on the ΔS surface and the negative vector of
express the beam water collision kerma at the corresponding phantom surface element (ΔS) (equation 43); ΔS is defined as the size of the area element on the phantom surface, which faces the source (S) without interception by the phantom; θS is the angle between the normal vector line on the ΔS surface and the negative vector of ![]() ; G(Ajaw) expresses the electron contamination factor as a function of the jaw field (Ajaw) [6, 7]. Γ1 and Γ2 are introduced to improve the G function, which can apply only to open jaw fields and only to electrons streaming along the ray lines emanating from the source (S).
; G(Ajaw) expresses the electron contamination factor as a function of the jaw field (Ajaw) [6, 7]. Γ1 and Γ2 are introduced to improve the G function, which can apply only to open jaw fields and only to electrons streaming along the ray lines emanating from the source (S).
Γ1 represents the degree of attenuation of the contaminant electrons when penetrating the MLC and wedge filter along the position vector LΔS. Let Γ1 be formulated using penetration features of the secondary electrons produced by EN photons as

where H1(Ξ, R; EN) expresses the in-water forward primary dose kernel to point (Ξ, R) produced by EN photons (refer to Appendix A); and Teff (EN) is the total effective thickness for the MLC and wedge devices, evaluated along the position vector LΔS as a function of EN. It is calculated as
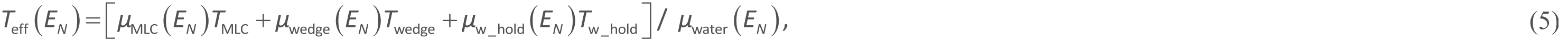
where µMLC(EN), µwedge(EN), µw_hold(EN) and µwater(EN) are the linear attenuation coefficients of the MLC, wedge filter, wedge holder and water, respectively, for EN photons; and TMLC, Twedge and Tw_hold are the thicknesses of the MLC, wedge filter and wedge holder, respectively, measured along the position vector LΔS.
Γ1 is introduced to improve the accuracy of the calculation at points very near the phantom surface [7], to take into account the dose delivered by the contaminant electrons coming across the ray lines. For phantoms constructed of water-like media, we express Γ2 as

Where ![]() is the relative electron density averaged between point P and the ΔS center (however, it has been found [13, 15] that the contamination dose does not vary simply in proportion to the beam water collision kerma of
is the relative electron density averaged between point P and the ΔS center (however, it has been found [13, 15] that the contamination dose does not vary simply in proportion to the beam water collision kerma of ![]() .
.
In regard to the calculated dose to point P(XC, YC, ZC) in the phantom (Figure 2), it can be understood that the primary and scatter doses emanating from the volume elements in the phantom are generally composed of forward and backward dose components, that the primary and scatter doses emanating from volume elements in the wedge and MLC devices are composed only of forward dose components because these devices are placed relatively far above the phantom, and that the contamination dose is generally composed of forward and backward dose components. Appendix A defines in-water primary and scatter dose kernels as H1(Ξ, R; EN), H2(Η, R; EN), K1(Ξ, R; EN) and K2(Ξ, R; EN) using orthogonal coordinates (Ξ, R) and (H, R) for incident EN photons.
Next, we examine the dose kernels of hphan, hwedge, hw_hold, hMLC, kphan, kwedge, kw_hold and kMLC (equations 1-3) used in the unified irradiated body. According to the aforementioned density scaling theorem, the coordinates of ξ, η, r, ξs, ηs and rs shown in Figure 3 can be converted to the in-water coordinates as:
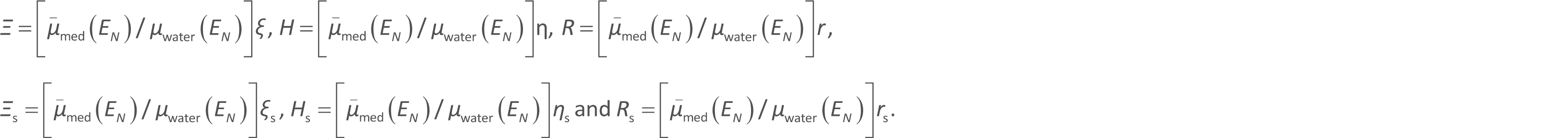
Then, the dose kernels in equations 1-3 can be evaluated by employing the in-water dose kernels (H1,2 and K1,2 ) as follows (also refer to the angles of θphan, θS, θwedge, θw_hold and θMLC in Figure 2):
(a) hphan in equation 1 is one of the following two kernels:


where ![]() is evaluated along the line connecting P and the effective point within the ΔV element; and Fhetero is a correction factor [6, 7] for phantom heterogeneity. This correction factor is simply used only for forward primary dose calculations, not as a function of EN. We should set Fhetero = 1 for homogeneous phantoms.
is evaluated along the line connecting P and the effective point within the ΔV element; and Fhetero is a correction factor [6, 7] for phantom heterogeneity. This correction factor is simply used only for forward primary dose calculations, not as a function of EN. We should set Fhetero = 1 for homogeneous phantoms.
(b) kphan in equation 2 is one of the following two kernels:


(c) hphan in equation 3 is one of the following two kernels:


where ![]() is evaluated along the line connecting P and the center of ΔS.
is evaluated along the line connecting P and the center of ΔS.
(d) hwedge and kwedge (used as θwedge < π/2) in equations 1 and 2 are, respectively,


where Fwedge_p and Fwedge_s are the correction factors, respectively, for the calculation of the primary and scatter dose components, not as a function of EN. We express them as


with ![]() , where αwedge_p = 2.5 × 10-2, βwedge_p = 0.5, αwedge_p = 7.0 × 10-8, βwedge_p = 0.5 and γwedge_s = 50 for each of the 15°, 30°, 45° and 60° wedges (wedge types 1–4) (these values, without units, were derived by comparing the calculated and measured dose datasets).
, where αwedge_p = 2.5 × 10-2, βwedge_p = 0.5, αwedge_p = 7.0 × 10-8, βwedge_p = 0.5 and γwedge_s = 50 for each of the 15°, 30°, 45° and 60° wedges (wedge types 1–4) (these values, without units, were derived by comparing the calculated and measured dose datasets).
(e) hw_hold and kw_hold (used as θw_hold < π/2) in equations 1 and 2 are, respectively,


(f) hMLC and kMLC (used as θMLC < π/2) in equations 1 and 2 are, respectively,


where FMLC_p and FMLC_s are the correction factors, respectively, for the calculation of the primary and scatter dose components emanating from the MLC, not as functions of EN. We express them as


with ![]() , where we let αMLC_p = 1 × 10-3, βMLC_p = 1.5, αMLC_s = 100, βMLC_s = 1.5 and γMLC_s = 1.0 (these values without units were derived by comparing the calculated and measured dose datasets).
, where we let αMLC_p = 1 × 10-3, βMLC_p = 1.5, αMLC_s = 100, βMLC_s = 1.5 and γMLC_s = 1.0 (these values without units were derived by comparing the calculated and measured dose datasets).

Modeling the jaw collimator, MLC and wedge devices
The jaw collimator, MLC and wedge devices are 3D objects (Figure 4a). However, to simplify the calculation of the in-air beam intensity with an open jaw field or with an open MLC field under a jaw field, and to also simplify the calculation of the dose that the phantom receives from the MLC and wedge, we treated the jaws, MLC and wedge as two-dimensional (2D) structures. That is, we treated them as plates with no geometrical thickness (Figure 4b). The following describes the details of the jaws, MLC and wedge plates:
(a) The jaw collimator is simulated by four plates that are perpendicular to the isocenter axis. They are located at four positions: Zbeam = Zupper_1(≅72.0 cm), Zbeam = Zupper_2(≅72.0 cm), Zbeam = Zlower_1(≅ 63.3 cm) and Zbeam = Zlower_2(≅ 63.3 cm). The Zupper_1 and Zupper_2 positions coincide with the corresponding top edges of the upper-1 and -2 jaws, respectively, and the Zlower_1 and Zlower_2 positions coincide with the corresponding top edges of the lower -1 and -2 jaws, respectively. We assume that these four plates form the same irradiation field on the isocenter plane as the real jaws do, and that the radiation emanating from the source (S) is perfectly shielded by the plates. This replacement is performed [6] to calculate in a simple manner the in-air beam intensity caused by the extended radiation source on the X-ray target plane and the extended radiation source on the flattening-filter plane. It should be noted that this replacement causes a slight inconvenience for the calculation of the in-air beam intensity outside the jaw field (refer to the circle mark in Figure 5b as described later).
(b) The MLC is simulated by a plate perpendicular to the isocenter axis at the position Zbeam = ZMLC (= 53.7 cm, which was determined by analyzing the measured MLC-Sc datasets shown in Figure 6 below). We let the plate form the same MLC field as the MLC does on the isocenter plane, corresponding to the MLC effective thicknesses along ray lines emanating from the source (S). This dataset is used to calculate the in-air beam intensity for the open MLC field. It is also used for calculating the dose that the phantom receives from the MLC.
(c) Each of the wedges (15°, 30°, 45° and 60°) and their 0.2 cm acrylic holder are replaced with a plate perpendicular to the isocenter axis at the fixed position Zbeam = Zwedge (= 42.4 cm), which is the same as the position of the boundary surface of the wedge and its holder. We let the plate form the wedge field as the wedge device does on the isocenter plane, corresponding to the wedge filter and wedge holder thicknesses along ray lines emanating from the source (S). This dataset is used to calculate the dose that the phantom receives from the wedge device and the in-air beam intensity under the wedge-filtered jaw or MLC field.
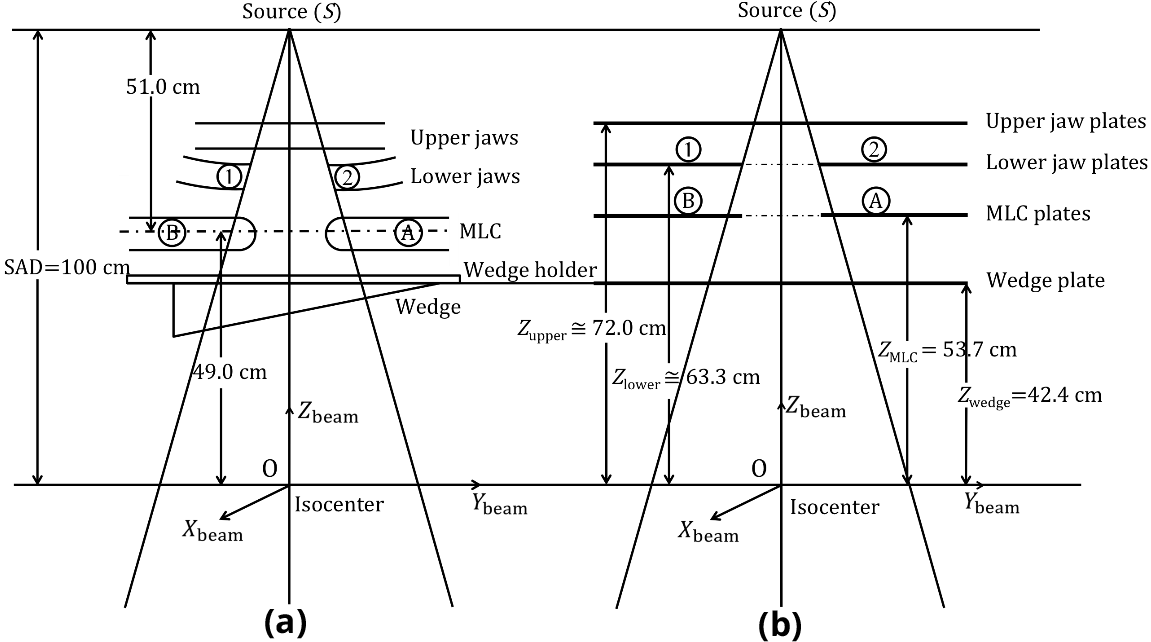
In-air output factor calculation for open MLC fields
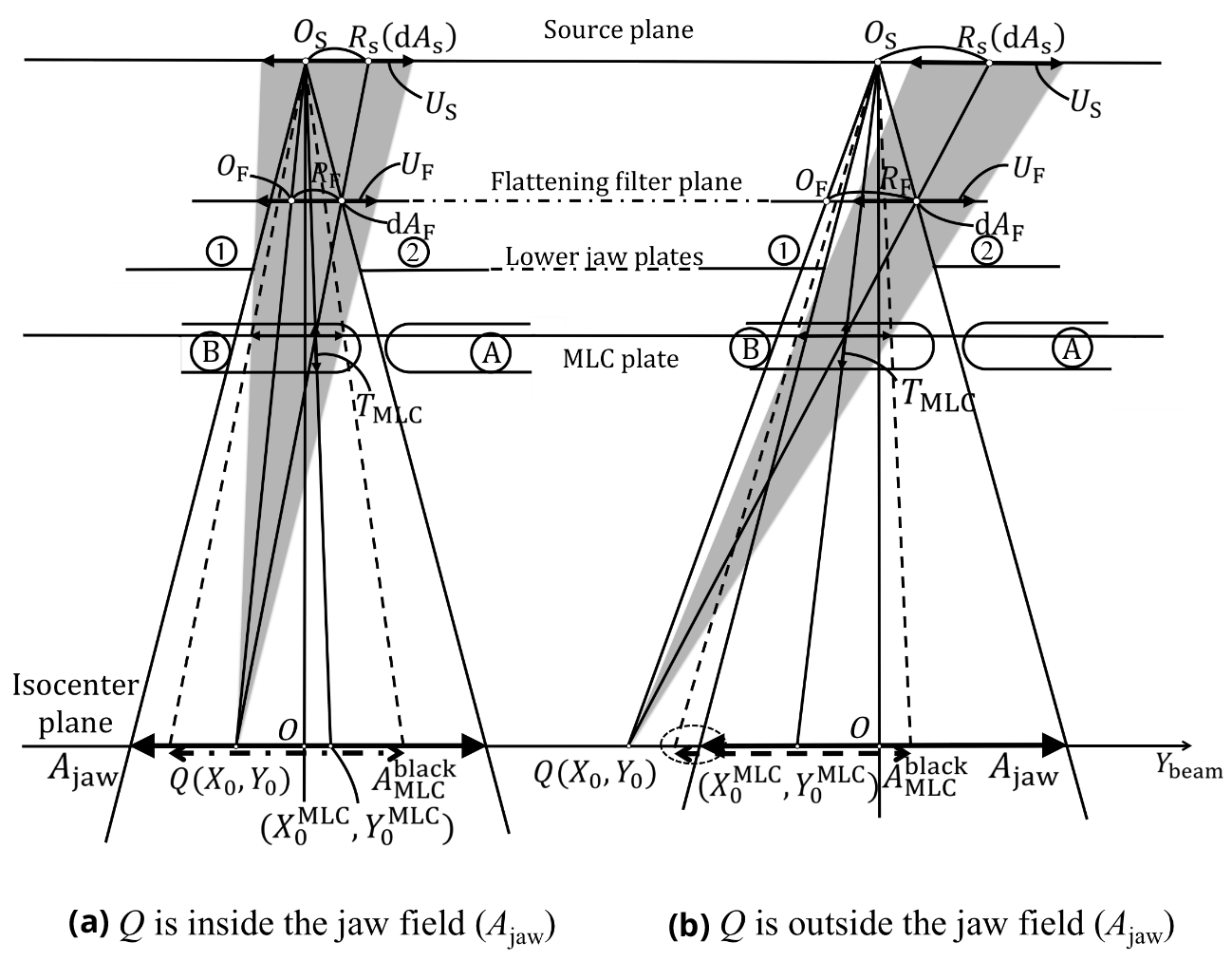
We describe how to calculate the in-air beam intensity for an open MLC field under a given jaw field (without wedge filtration). The calculation is based on the MLC leaf-field output subtraction method [16] at the 15th ICCR. The details are; Zhu and Bjärngard [17] and Zhu and colleagues [18-20] introduced the 2D Gaussian-source model for the extended radiation source only with a flattening filter to calculate the in-air output factor (Sc) [21, 22] for open jaw or MLC fields. Later, Iwasaki and colleagues [6] proposed the use of this model not only for the flattening filter but also for the X-ray target (or the source (S). It was found that using the two extended radiation sources was effective, even around a zero-area jaw field under conditions of lateral electron disequilibrium. We propose using the two extended radiation sources model to calculate the in-air output factor (OPFin_air) for an open MLC field under a given jaw field by subtracting the in-air output reduction caused by setting the MLC field to the jaw field from the in-air output for the open jaw field (let the in-air output reduction be designated the negative or “black” in-air output). This calculation method can take into account the delicate in-air output variations caused by the MLC leaf curvature and chamfers at the leaf end and the MLC interleaf X-ray leakage.
Figure 5 shows the calculation of the OPFin_air factor at a point Q (X0,Y0) on the isocenter plane for an open MLC field (AMLC) under a given jaw field (Ajaw), where Figures 5a, b are drawn for the cases where point Q is inside and outside the Ajaw field, respectively. An extended radiation source exists around point OS (coinciding with the center of the X-ray target) on the source plate; and another extended radiation source is assumed to exist around point OF at the intersection of the flattening-filter plate and the ray line connecting points OS and Q. On the isocenter plane, we introduce a special field called a black MLC field ![]() , which is used to evaluate the amount of negative (or black) in-air output, (where the dashed lines in Figures 5a, b are drawn by taking into account the positions of the lower jaw plates (in like manner, another set of dashed lines should also be utilized by taking into account the positions of the upper jaw plates)). It should be emphasized that, if point Q is outside the Ajaw field, the
, which is used to evaluate the amount of negative (or black) in-air output, (where the dashed lines in Figures 5a, b are drawn by taking into account the positions of the lower jaw plates (in like manner, another set of dashed lines should also be utilized by taking into account the positions of the upper jaw plates)). It should be emphasized that, if point Q is outside the Ajaw field, the ![]() field does not contain point Q. In this case, as indicated by the circle mark in Figure 5b, the
field does not contain point Q. In this case, as indicated by the circle mark in Figure 5b, the ![]() field extends beyond the Ajaw field edge. Such an extended region is caused by the treatment of the 2D jaw-collimator plates (the irradiation geometry tells us that, if the real 3D jaw collimator can be utilized, no such large
field extends beyond the Ajaw field edge. Such an extended region is caused by the treatment of the 2D jaw-collimator plates (the irradiation geometry tells us that, if the real 3D jaw collimator can be utilized, no such large ![]() fields can be generated).
fields can be generated).
We normalize the OPFin_air factor to unity at the isocenter with an open jaw field of Ajaw = 10 × 10 cm2 (= 10 × 10iso), whose center coincides with the isocenter. Then, the OPFin_air factor at point Q (X0,Y0) for an open AMLC field under a given Ajaw field can be calculated as
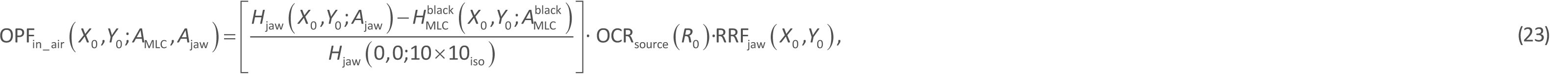
with ![]() , where OCRsource (R0) is the source off-center ratio [6], obtained by assuming that it is a function of only R0 for an open infinite Ajaw field (defined as the in-air beam intensity (in water collision kerma) at a point that is R0 distant from the isocenter to that at the isocenter (that is, OCRsource(0) = 1), where the OCRsource dataset was produced by applying an in-air chamber response function [4] of
, where OCRsource (R0) is the source off-center ratio [6], obtained by assuming that it is a function of only R0 for an open infinite Ajaw field (defined as the in-air beam intensity (in water collision kerma) at a point that is R0 distant from the isocenter to that at the isocenter (that is, OCRsource(0) = 1), where the OCRsource dataset was produced by applying an in-air chamber response function [4] of ![]() to an in-air dose dataset measured only at points of Ybeam ≥ 0 on the Ybeam axis). RRFjaw is the jaw-collimator radiation reflection factor [6], letting RRFjaw = 1 and RRFjaw > 1, respectively, inside and outside the Ajaw field. For beams with no MLC device, we obtain
to an in-air dose dataset measured only at points of Ybeam ≥ 0 on the Ybeam axis). RRFjaw is the jaw-collimator radiation reflection factor [6], letting RRFjaw = 1 and RRFjaw > 1, respectively, inside and outside the Ajaw field. For beams with no MLC device, we obtain ![]() by setting AMLC = ∞ (infinite field) and
by setting AMLC = ∞ (infinite field) and ![]() in equation 23 (see Appendix C for definitions of “off-center jaw-Sc factor”, “MLC-Sc factor” and “jaw-Sc factor”).
in equation 23 (see Appendix C for definitions of “off-center jaw-Sc factor”, “MLC-Sc factor” and “jaw-Sc factor”).
First, we formulate [6] Hjaw in equation 23 as



where ![]() is the side of the equivalent square field for Ajaw; and a1, a2, λS and λF are constants, where it is assumed that a1 (the monitor-backscatter coefficient) is influenced only by the jaw collimator, which forms the Ajaw field, and not by the MLC or by the wedge. For the present 10-MV X-ray accelerator, we have obtained a1 = 0.00146 cm-1, a2 = 0.0830, λS = 0.299 cm and λS = 3.097 cm. It can be understood that Hjaw approaches zero as the Ajaw field approaches zero.
is the side of the equivalent square field for Ajaw; and a1, a2, λS and λF are constants, where it is assumed that a1 (the monitor-backscatter coefficient) is influenced only by the jaw collimator, which forms the Ajaw field, and not by the MLC or by the wedge. For the present 10-MV X-ray accelerator, we have obtained a1 = 0.00146 cm-1, a2 = 0.0830, λS = 0.299 cm and λS = 3.097 cm. It can be understood that Hjaw approaches zero as the Ajaw field approaches zero.
Next, we formulate [16] ![]() in equation 23 as
in equation 23 as

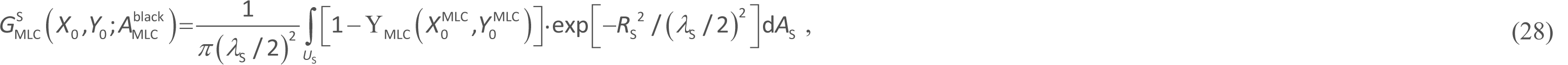
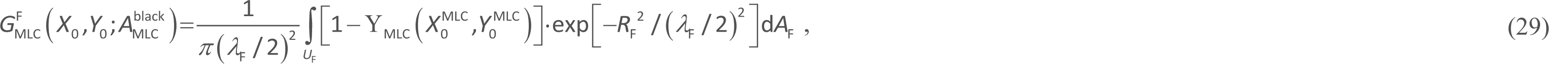
where point ![]() should be within the
should be within the ![]() region (Figure 5a,b show how point Q, area element dAS (or dAF), point OS and point
region (Figure 5a,b show how point Q, area element dAS (or dAF), point OS and point ![]() are related); and γMLC is the MLC attenuation factor, evaluated using the beam water collision kerma along the ray line connecting points OS and
are related); and γMLC is the MLC attenuation factor, evaluated using the beam water collision kerma along the ray line connecting points OS and ![]() as
as
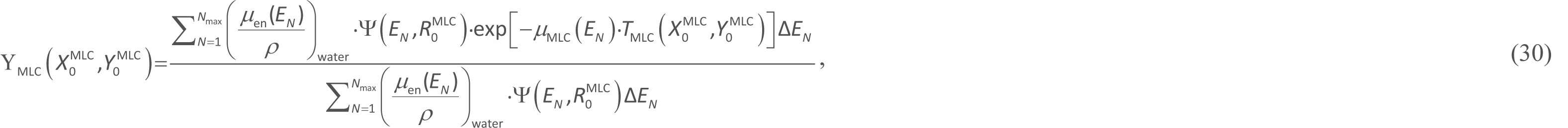
with ![]() , where TMLC is the MLC effective thickness measured along the ray line connecting points OS and
, where TMLC is the MLC effective thickness measured along the ray line connecting points OS and ![]() (it should be noted that we obtain γMLC = 1 for TMLC = 0); (μen (EN)/ρ)water is the mass energy absorption coefficient of water for EN photons; and
(it should be noted that we obtain γMLC = 1 for TMLC = 0); (μen (EN)/ρ)water is the mass energy absorption coefficient of water for EN photons; and ![]() expresses the energy fluence spectrum for an open infinite jaw field, as a function of the energy bin (EN)and the off-axis distance
expresses the energy fluence spectrum for an open infinite jaw field, as a function of the energy bin (EN)and the off-axis distance ![]() (Figure 7), normalized as
(Figure 7), normalized as ![]() .
.
If TMLC = 0 for all points on the isocenter plane, we have ![]() (that is, no MLC setting for the Ajaw field). Ideally, YMLC should be evaluated along the line connecting point Q and dAS (or dAF). However, we did not use this procedure, because, along such a line, the spectrum estimation has not yet been established, and calculation of the effective thickness of the MLC is very complicated.
(that is, no MLC setting for the Ajaw field). Ideally, YMLC should be evaluated along the line connecting point Q and dAS (or dAF). However, we did not use this procedure, because, along such a line, the spectrum estimation has not yet been established, and calculation of the effective thickness of the MLC is very complicated.
The total in-air energy fluence
For an open infinite jaw field yielding an in-air water collision kerma of OCRsource(R0) on the isocenter plane (equation 23), the total in-air energy fluence ![]() at point (X0,Y0) can be evaluated as
at point (X0,Y0) can be evaluated as

with ![]() . It should be noted that the denominator of equation 31 expresses the total water collision kerma that the normalized energy fluence spectrum yields at the corresponding point in air. Therefore, the in-air energy fluence related to the normalized energy fluence of Ψ(EN, R0) ΔEN yields the following in-air water collision kerma:
. It should be noted that the denominator of equation 31 expresses the total water collision kerma that the normalized energy fluence spectrum yields at the corresponding point in air. Therefore, the in-air energy fluence related to the normalized energy fluence of Ψ(EN, R0) ΔEN yields the following in-air water collision kerma:

The in-phantom dose calculations described below are carried out using the ![]() function. If a wedge filters the open jaw or MLC field, we calculate the in-air water collision kerma variation for each set of primary EN photons (N = 1 to Nmax), depending on the wedge thickness along the corresponding ray line. This is because the in-phantom dose is calculated by using the primary photons emitted from the source (S) and by treating the phantom, the wedge and the MLC as parts of a unified irradiation body.
function. If a wedge filters the open jaw or MLC field, we calculate the in-air water collision kerma variation for each set of primary EN photons (N = 1 to Nmax), depending on the wedge thickness along the corresponding ray line. This is because the in-phantom dose is calculated by using the primary photons emitted from the source (S) and by treating the phantom, the wedge and the MLC as parts of a unified irradiation body.
Calculation of ![]()
This section is described mainly by referring to figures 4, 5, 8, and 9, where the 2D wedge and MLC plates are placed at Zbeam = Zwedge and Zbeam = ZMLC respectively. We set up the precondition that the 2D wedge and MLC plates hold data regarding the thicknesses (or effective thicknesses) of the 3D wedge and the MLC devices, respectively, measured along the ray lines emanating from the source (S). In the inserted diagram on the right in Figure 8, we let T0 denote the thickness (or effective thickness) measured along a ray line passing through a point ![]() on the wedge or MLC plate and through a point Q(X0,Y0) on the isocenter plane, and let α1 denote the angle between the ray line and the isocenter plane. Then the thickness (or effective thickness) along the line that is parallel to the Zbeam axis and passes through the point
on the wedge or MLC plate and through a point Q(X0,Y0) on the isocenter plane, and let α1 denote the angle between the ray line and the isocenter plane. Then the thickness (or effective thickness) along the line that is parallel to the Zbeam axis and passes through the point ![]() can be approximated as T0 sinα1. Draw an axis r' from a dose calculation point P(XC, YC, ZC) that passes through the point
can be approximated as T0 sinα1. Draw an axis r' from a dose calculation point P(XC, YC, ZC) that passes through the point ![]() . Then the thickness (or effective thickness) measured along the r' axis can be approximated as T0 sinα1/sinα2, where α2 is the angle between the r' axis and the isocenter plane. On the basis of this procedure, the following describes how to handle the 3D wedge and MLC devices.
. Then the thickness (or effective thickness) measured along the r' axis can be approximated as T0 sinα1/sinα2, where α2 is the angle between the r' axis and the isocenter plane. On the basis of this procedure, the following describes how to handle the 3D wedge and MLC devices.
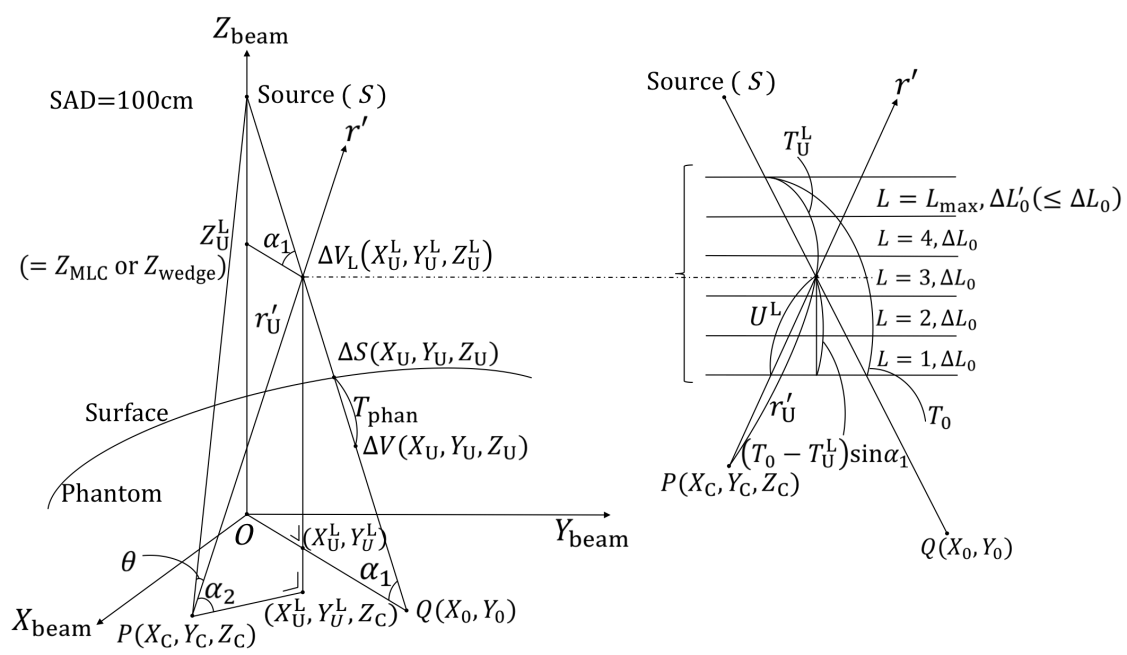
First, we refer to the thickness (or effective thickness) measured from the bottom side along the r' axis using the symbol UL (L = 1 to Lmax). The diagram shows the case when Lmax = 5 with equal interval sections ΔL0 and a residual section ΔL0 (≤ ΔL'0) along a line parallel to the Zbeam axis. We estimate the value for UL as

with



It should be noted that, at least for wedge filters, the calculation for UL is a close approximation because they are constructed with continuously gentle slope faces against the isocenter plane.
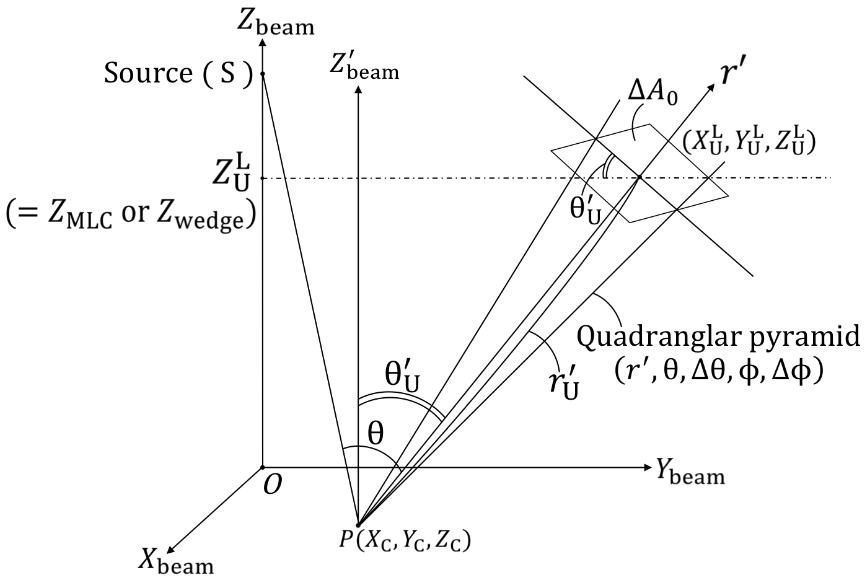
Second, at the point ![]() in the Lth section (Figures 8 and 9), we set an imaginary volume element (ΔVL) that is surrounded both by the ΔL0 or ΔL'0 layer faces and by the quadrangular pyramid faces determined by (r', θ, Δθ, φ, Δφ) whose apex is located at point P(XC, YC, ZC). Let ΔA0 denote the area of the pyramid base at the point
in the Lth section (Figures 8 and 9), we set an imaginary volume element (ΔVL) that is surrounded both by the ΔL0 or ΔL'0 layer faces and by the quadrangular pyramid faces determined by (r', θ, Δθ, φ, Δφ) whose apex is located at point P(XC, YC, ZC). Let ΔA0 denote the area of the pyramid base at the point ![]() perpendicular to the r' axis; r'U denotes the distance between points P(XC, YC, ZC) and
perpendicular to the r' axis; r'U denotes the distance between points P(XC, YC, ZC) and ![]() and θ'U denotes the angle between the Zbeam axis (or the Z'beam axis starting at point P and parallel to the Zbeam axis) and the r' axis. Then the magnitude of (ΔVL) is given as
and θ'U denotes the angle between the Zbeam axis (or the Z'beam axis starting at point P and parallel to the Zbeam axis) and the r' axis. Then the magnitude of (ΔVL) is given as


with

To calculate the primary and scatter doses from the wedge and MLC bodies, we used ΔL0 = 0.01 cm and ΔL0 = 0.1 cm, respectively. To calculate both the primary and scatter doses from the wedge holder, we used ΔL0 = 0.2 cm (that is, Lmax = 1 in Figure 8). The value of T0 measured along each ray line was obtained by analyzing the manufacturer’s diagrams. However, we assumed that each of the MLC leaves had no driving screw holes (0.33 cm and 0.43 cm in diameter for the 0.5 cm and 1 cm wide leaves, respectively).
Next, we describe the calculation of the beam water collision kermas of ![]() (equations 1-3) for a given volume element (ΔV or ΔVL) or a given area element ΔS within the unified irradiated body (Figure 8). Because the X-ray emission from the flattening filter is very small relative to that from the X-ray target (for the present 10-MV X-ray accelerator, the strength ratio of the extra radiation source to the X-ray target for an infinite Ajaw field is α2 = 0.0830 (equation 24), we assumed that all X-rays emanate from the source (S).
(equations 1-3) for a given volume element (ΔV or ΔVL) or a given area element ΔS within the unified irradiated body (Figure 8). Because the X-ray emission from the flattening filter is very small relative to that from the X-ray target (for the present 10-MV X-ray accelerator, the strength ratio of the extra radiation source to the X-ray target for an infinite Ajaw field is α2 = 0.0830 (equation 24), we assumed that all X-rays emanate from the source (S).
It has been found that, particularly under MLC field irradiation, the OPFin_air factor (equation 23) determined on the basis of a single point within each ΔV element in the phantom cannot give accurate dose calculation results. This is mainly caused by the nonuniformity of the beam intensities within each ΔV element owing to the use of the MLC. In the following dose calculation procedures, the symbol ![]() is used when the beam intensity for each ΔV element in the phantom should be evaluated based on the beam intensity at a single point within each ΔV element. On the other hand, the symbol
is used when the beam intensity for each ΔV element in the phantom should be evaluated based on the beam intensity at a single point within each ΔV element. On the other hand, the symbol ![]() is used when the in-air beam intensity for each ΔV element in the phantom should be evaluated based on the beam intensities at multiple points within each ΔV element (the details will be described later in equation 47).
is used when the in-air beam intensity for each ΔV element in the phantom should be evaluated based on the beam intensities at multiple points within each ΔV element (the details will be described later in equation 47).
Here we classify the wedge irradiation mode using wedge types = 0 to 4, stipulating that wedge type = 0 signifies irradiation with no wedge (that is, open jaw or MLC field irradiations), and wedge types 1, 2, 3 and 4 denote jaw or MLC field irradiations with the use of a 15°, 30°, 45° and 60° wedge, respectively. Under these conditions, the following (a)-(e) describe the evaluation of the beam intensity for a point ![]() (L = 1 to Lmax) within the MLC or wedge, or for a point (XU, YU, ZU) on the phantom surface or within the phantom (Figure 8), these points are on a ray line passing through point Q(X0,Y0) on the isocenter plane).
(L = 1 to Lmax) within the MLC or wedge, or for a point (XU, YU, ZU) on the phantom surface or within the phantom (Figure 8), these points are on a ray line passing through point Q(X0,Y0) on the isocenter plane).
(a) For the beam intensity calculation within the MLC device, we set ![]() (= 53.7 cm), which is determined by analyzing calculated and measured MLC-Sc datasets (Figure 6). The
(= 53.7 cm), which is determined by analyzing calculated and measured MLC-Sc datasets (Figure 6). The ![]() collision kerma caused by the EN photons for the ΔVL element at the point
collision kerma caused by the EN photons for the ΔVL element at the point ![]() in the Lth section of the MLC plate should be evaluated only under a given Ajaw opening, because the MLC device is placed in close proximity to the jaw collimator; that is, an MLC field of AMLC = ∞ should be used to evaluate
in the Lth section of the MLC plate should be evaluated only under a given Ajaw opening, because the MLC device is placed in close proximity to the jaw collimator; that is, an MLC field of AMLC = ∞ should be used to evaluate ![]() in the following equation. Therefore, the calculation is performed as follows:
in the following equation. Therefore, the calculation is performed as follows:
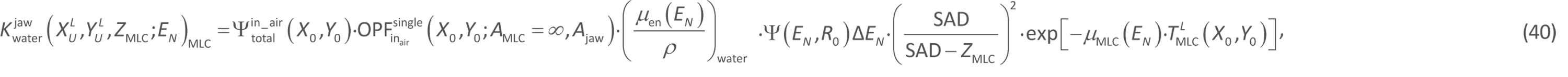
where SAD (= 100 cm) is the source–axis distance (or the distance between the source (S) and the isocenter plane); ![]() is the effective thickness of the MLC, measured along the corresponding ray line (Figure 8) from the MLC top side to the middle point
is the effective thickness of the MLC, measured along the corresponding ray line (Figure 8) from the MLC top side to the middle point ![]() of the Lth section; and μMLC(EN) is the linear attenuation coefficient of the MLC material for EN photons.
of the Lth section; and μMLC(EN) is the linear attenuation coefficient of the MLC material for EN photons.
(b) For the beam intensity calculation within the wedge holder, we set ![]() (= 42.4 cm) with L = 1 (= Lmax; Figure 8). The
(= 42.4 cm) with L = 1 (= Lmax; Figure 8). The ![]() collision kerma caused by the EN photons for the ΔVL element at the point
collision kerma caused by the EN photons for the ΔVL element at the point ![]() in the Lth section of the wedge holder should also be evaluated only under a given Ajaw opening (that is, an MLC field of AMLC = ∞ should be used for
in the Lth section of the wedge holder should also be evaluated only under a given Ajaw opening (that is, an MLC field of AMLC = ∞ should be used for ![]() in the following equation). Therefore, the calculation is performed as follows:
in the following equation). Therefore, the calculation is performed as follows:
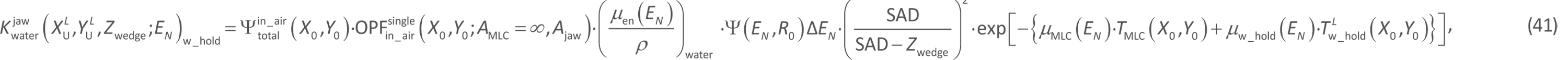
where TMLC(X0,Y0) is the thickness of the MLC, measured along the corresponding ray line (Figure 8); ![]() is the wedge-holder thickness (equation 35) measured along the corresponding ray line, from the wedge-holder top side to the middle point
is the wedge-holder thickness (equation 35) measured along the corresponding ray line, from the wedge-holder top side to the middle point ![]() of the Lth section; and μw_hold(EN) is the linear attenuation coefficient of the wedge-holder material for the EN photons. For the case of no MLC in the beam, we should set TMLC(X0,Y0) = 0.
of the Lth section; and μw_hold(EN) is the linear attenuation coefficient of the wedge-holder material for the EN photons. For the case of no MLC in the beam, we should set TMLC(X0,Y0) = 0.
(c) For the beam intensity calculation within the wedge body, we set ![]() (= 42.4 cm) with L = 1, 2, ....., Lmax (Figure 8). The
(= 42.4 cm) with L = 1, 2, ....., Lmax (Figure 8). The ![]() collision kerma caused by the EN photons for the ΔVL element at the point
collision kerma caused by the EN photons for the ΔVL element at the point ![]() in the Lth section of the wedge body should also be evaluated only under a given Ajaw opening (that is, AMLC = ∞ should be used for
in the Lth section of the wedge body should also be evaluated only under a given Ajaw opening (that is, AMLC = ∞ should be used for ![]() in the following equation). Therefore, the calculation is performed as follows:
in the following equation). Therefore, the calculation is performed as follows:

where ![]() is the wedge-body thickness (equations 34 and 35) measured along the corresponding ray line, from the wedge-body top side to the middle point
is the wedge-body thickness (equations 34 and 35) measured along the corresponding ray line, from the wedge-body top side to the middle point ![]() of the Lth section; and μwedge(EN) is the linear attenuation coefficient of the wedge-body material for the EN photons. For the case of no MLC in the beam, we should set TMLC(X0,Y0) = 0.
of the Lth section; and μwedge(EN) is the linear attenuation coefficient of the wedge-body material for the EN photons. For the case of no MLC in the beam, we should set TMLC(X0,Y0) = 0.
(d) For the beam intensity calculation for the ΔS element at the point (XU, YU, ZU) on the phantom surface, we should take into account the AMLC field under a given Ajaw opening. Under the condition that the wedge generally covers the beam, we let the ![]() collision kerma for ΔS caused by EN photons be calculated as follows:
collision kerma for ΔS caused by EN photons be calculated as follows:

with


where ![]() is the field area that the MLC collimator forms inside the Ajaw field on the isocenter plane (that is,
is the field area that the MLC collimator forms inside the Ajaw field on the isocenter plane (that is, ![]() ); TMLC(X0,Y0) is the effective thickness of the MLC, measured along the corresponding ray line (note that, for any ray line within the MLC field, we should set TMLC(X0,Y0) = 0);
); TMLC(X0,Y0) is the effective thickness of the MLC, measured along the corresponding ray line (note that, for any ray line within the MLC field, we should set TMLC(X0,Y0) = 0); ![]() is a factor introduced to make a small correction for the beam intensity calculation by employing
is a factor introduced to make a small correction for the beam intensity calculation by employing ![]() , given as a function of both
, given as a function of both ![]() and the wedge type (Appendix D);
and the wedge type (Appendix D); ![]() is a factor introduced to correct for the beam intensity calculation, given as a function of TMLC(X0,Y0) and
is a factor introduced to correct for the beam intensity calculation, given as a function of TMLC(X0,Y0) and ![]() , finely adjusting the degree of X-ray penetration when passing through the MLC effective thickness of TMLC(X0,Y0) along the corresponding ray line; and Tw_hold(X0,Y0) and Twedge(X0,Y0) are the thicknesses of the wedge holder and the wedge body, respectively, measured along the ray line (for the case of no wedge device in the beam, we should set Tw_hold(X0, Y0) = Twedge(X0, Y0) = 0.
, finely adjusting the degree of X-ray penetration when passing through the MLC effective thickness of TMLC(X0,Y0) along the corresponding ray line; and Tw_hold(X0,Y0) and Twedge(X0,Y0) are the thicknesses of the wedge holder and the wedge body, respectively, measured along the ray line (for the case of no wedge device in the beam, we should set Tw_hold(X0, Y0) = Twedge(X0, Y0) = 0.
(e) To calculate the beam intensity for the ΔV element at the point (XU, YU, ZU) within the phantom, we should also take into account the AMLC field under a given Ajaw opening. Here, it should be noted that the ray line passing through the point (X0, Y0) on the isocenter plane should also pass through the effective point (Figure 2b) within the ΔV element. It has been found that the same ![]() and
and ![]() factors as before should be used to make small corrections also for the beam intensity calculation by employing
factors as before should be used to make small corrections also for the beam intensity calculation by employing ![]() . Assuming that the wedge generally covers the beam, we let the
. Assuming that the wedge generally covers the beam, we let the ![]() collision kerma for ΔV caused by the EN photons are calculated as follows:
collision kerma for ΔV caused by the EN photons are calculated as follows:
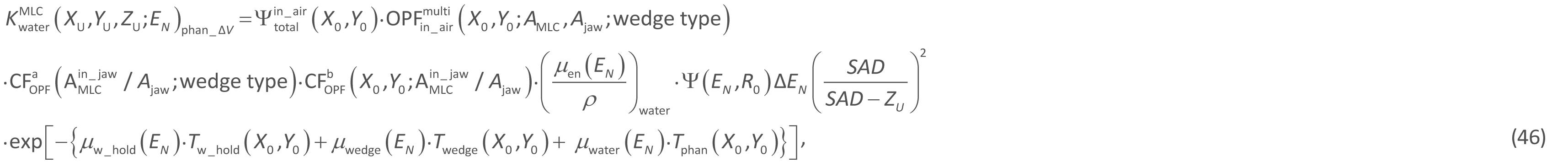
where, assuming that the phantom is constructed of water-equivalent media, Tphan(X0, Y0) is the effective thickness of the phantom, measured along the ray line from the phantom surface to the point (XU, YU, ZU) and μwater(EN) is the linear attenuation coefficient of water for the EN photons. For the case of no wedge device in the beam, we should set Tw_hold(X0, Y0) = Twedge(X0, Y0) = 0. The ![]() factor is experimentally constructed as
factor is experimentally constructed as

with



where λ0 = 1.25 (no units) for the irradiation mode of wedge type = 0 (that is, for open jaw and MLC fields), and λ0 = 3.50 for the irradiation modes of wedge type = 1-4 (that is, for wedge-filtered jaw and MLC fields). These λ0 values were obtained by comparing the calculated and measured percentage depth dose (PDD) and off-center ratio (OCR) datasets. This paper uses Jmax = 27 as the number of multiple points set within each ΔV element, through which ray lines of J = 1, 2,......, Jmax pass (nine points on each of the three planes set perpendicular to the r' axis (Figure 2b); and OPFJ is the OPFin_air factor (equation 23) at the point where the J ray line intersects the isocenter plane (Figure 2b). We have λOPF = 0 for ![]() for any wedge type. WOPF expresses the degree of nonuniformity of the incident beam intensity for a given ΔV element, determined by Ajaw, AMLC and wedge type. It should be noted that, in equation 47, we generally have
for any wedge type. WOPF expresses the degree of nonuniformity of the incident beam intensity for a given ΔV element, determined by Ajaw, AMLC and wedge type. It should be noted that, in equation 47, we generally have ![]() . It has been found that the work of the
. It has been found that the work of the ![]() factor becomes remarkable as the width of an MLC leaf-blocked section in a jaw field becomes narrow (Figures 10 and 11).
factor becomes remarkable as the width of an MLC leaf-blocked section in a jaw field becomes narrow (Figures 10 and 11).
Spectra and dose kernels
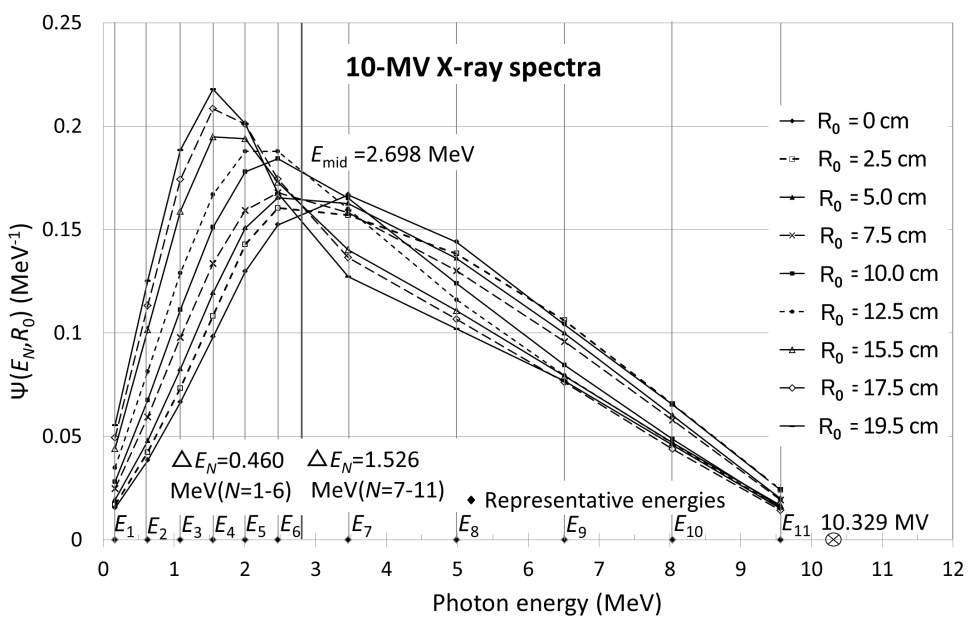
We reconstructed [3, 4] a new set of energy fluence spectra for the accelerator as follows. We measured sets of in-air transmission data at points on the Ybeam axis where Ybeam ≥ 0 using an ionization chamber with an acrylic buildup cap (a factor of fcap = 0.25 was assumed [4] to account for radiation attenuation and scatter in the buildup cap), in which we used acrylic attenuators of 0–30 cm in thickness and lead attenuators of 0-3 cm in thickness at off-axis distances of R0 = 0, 2.5, 5.0, 7.5, 10.0, 12.5, 15.5, 17.5 and 19.5 cm. We set a value of 10.329 MV for the accelerating voltage. Using a common set of energy bins for all the off-axis distances, we reconstructed a set of Ψ(EN, R0 ) spectra with an accuracy of approximately ±1% for the measured transmission data. The energy bins were E1 = 0.167 (= Emin), E2 = 0.627, E3 = 1.087, E4 = 1.548, E5 = 2.008, E6 = 2.468, E7 = 3.461, E8 = 4.987, E9 = 6.513, E10 = 8.040 and E11 = 9.566 MeV (= Emax) (namely, Nmax = 11 and Emid = 2.698 MeV with ΔEN = 0.460 MeV for N = 1–6, and with ΔEN = 1.526 MeV for N = 7–11). Figure 7 shows the reconstructed spectra at R0 = 0-19.5 cm. The X-ray spectrum becomes softer as the off-axis distance (R0) increases.
H1,2 and K1,2 dose kernels
Primary and scatter dose kernels in water (H1,2 and K1,2) for the energy bins of EN (N = 1 to 11) were produced through use of an Electron Gamma Shower (EGS) Monte Carlo code taking semi-infinite water phantoms (Figure A1). The primary and scatter dose kernels (as shown in Kimura and colleagues [7]) were produced, assuming the density of water to be unity.
Structure of the MLC
The MLC is made of a proprietary tungsten alloy. Accordingly, as an effective approach, we calculated the in-air output factor (OPFin_air) for an open MLC field using equation 23 by assuming that the MLC was composed of tungsten atoms; however, its density was different from that of pure tungsten metal. We let the ratio of the mass density of the MLC material to that of the pure tungsten material be ρMLC_factor = 0.897 This ratio was obtained by comparing calculated and measured MLC-Sc datasets (Figure 6), which we calculated by setting a virtual 2D MLC plate at a distance of ZMLC = 53.7 cm above the isocenter plane (Figure 4). On the whole, these numerical values gave the most accurate results for the MLC-Sc factor.
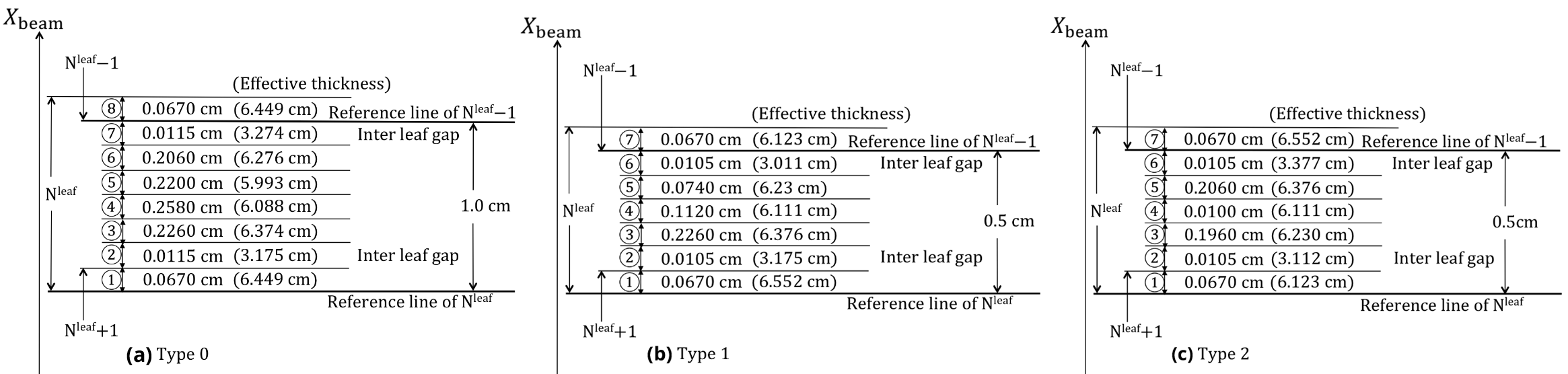
The MLC device is composed of sixty pairs of leaves. Let Nleaf denote the leaf number. At Nleaf = 1 and Nleaf = 60, each of the leaves forms a special shadow field 1.4 cm wide on the isocenter plane. At Nleaf = 2-10 and Nleaf = 51-59, each of the leaves forms a shadow field 1 cm wide, called a “full leaf” or “type 0.” At Nleaf = 11-50 forms a shadow field 0.5 cm wide, called a “half leaf.” The half leaves are classified into two types, type 1 and type 2, and these types are arrayed alternately. The full and half leaves have [23] a staple, a hook, a curved end, stepped sides and chamfers at both corners of the curved end so that these leaves can be moved to create an irregular field shape.
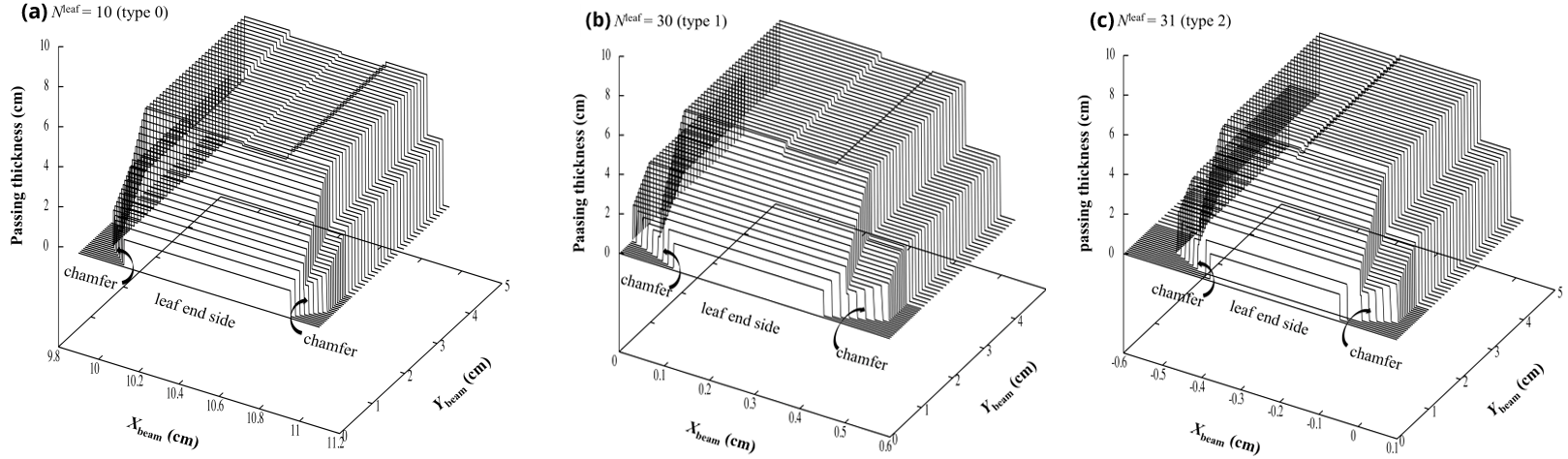
We analyzed the fine 3D structure of the full and half leaves as per the manufacturer’s information. When the full and half leaves are consecutively arrayed, the isocenter-axis components of the MLC effective thicknesses calculated along the ray lines are separated into seven or eight sections, respectively, in the direction of the Xbeam-axis (excluding the region around each curved end and ignoring the presence of the driving screw holes). Figure 12 illustrates the sectional widths measured on the isocenter plane for leaves of (a) type 0 (full), (b) type 1 (half) and (c) type 2 (half). The width of the region overlapped with the neighboring leaf is 0.067 cm; accordingly, each type has an actual width of 0.567 or 1.067 cm. The data in brackets give the isocenter-axis components. Figure 13 illustrates the 3D shapes of the isocenter-axis components for a single full or half leaf: (a) full leaf (type 0; using Nleaf = 10), (b) half leaf (type 1; using Nleaf = 30) and (c) half leaf (type 2; using Nleaf = 31). Note that the diagrams are drawn by setting the position of each leaf end at Ybeam = 0 cm.
MLC-Sc calculation
Using equation 23, we calculated the in-air output factor (OPFin_air) under a given set of AMLC and Ajaw fields along each center line of the seven or eight stripes using its sectional width (Figure 12) for each of the full or half MLC leaves. However, for Nleaf = 1 and 60 we assumed that each leaf had an infinite width, repeating the eight-striped pattern of the full leaf (to take into account the overrun area, as indicated by the circle in Figure 5b, when the Xbeam-axis side edge of the Ajaw field is nearly equal to ±20 cm). Moreover, to effectively calculate OPFin_air near the leaf end, we used a series of ΔTleaf steps on the middle line of each stripe, starting at the leaf end, as follows:

for i = 1, 2, 3, ......., where we let ![]() and
and ![]() . Then, we have
. Then, we have ![]() and
and ![]() (the step increases slowly at small and large values of i). For the experimental studies, we used
(the step increases slowly at small and large values of i). For the experimental studies, we used ![]() and
and ![]() .
.
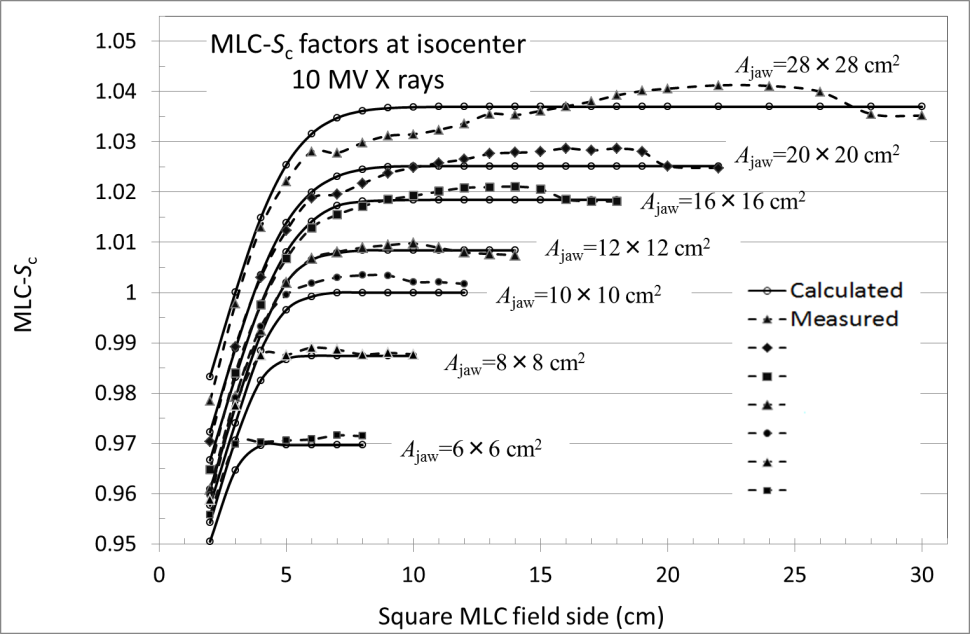
Figure 6 shows the calculated and measured MLC-Sc datasets that were obtained at the isocenter (X0 = Y0 = 0 cm) as a function of the square AMLC field side under each of the square Ajaw fields of 6 × 6 to 28 × 28 cm2 in size (equation C2 in Appendix C), letting both AMLC and Ajaw fields be symmetric with respect to the Xbeam and Ybeam axes, and letting the other pairs of A and B MLC leaves be closed at Ybeam = 0 cm. The measurement was performed using a cylindrical mini-phantom [24] with a 0.6 cm3 chamber (PTW 30006 Waterproof Farmer Chamber, Radiation Products Design, Inc. Albertville MN, USA) in free air. It can be seen that the measurement, having small waveforms for each of the Ajaw fields, seems to be influenced to a certain degree by scattered radiation from the MLC leaves.
The mean absolute deviation of the calculations is 0.21% (the minimum is -0.71% and the maximum is 0.68%). The MLC-Sc factor depends largely on the Ajaw field; however, under a given Ajaw field, the MLC-Sc factor rapidly decreases from a certain AMLC field size as the AMLC field becomes smaller. It should be noted that, when the positions of the pairs of closed leaves are set at Ybeam = ±30 cm, the mean absolute deviation of the calculations is 0.22% (the minimum is -0.77% and the maximum is 0.67%).Therefore, it is clear that the in-air output factor (OPFin_air) is influenced by the shapes of the MLC leaf structures. This is because the value of ![]() calculated by setting the positions of the closed leaves at Ybeam = ±30 cm is greater than that calculated with Ybeam = 0 cm.
calculated by setting the positions of the closed leaves at Ybeam = ±30 cm is greater than that calculated with Ybeam = 0 cm.
Structure of the wedge filters
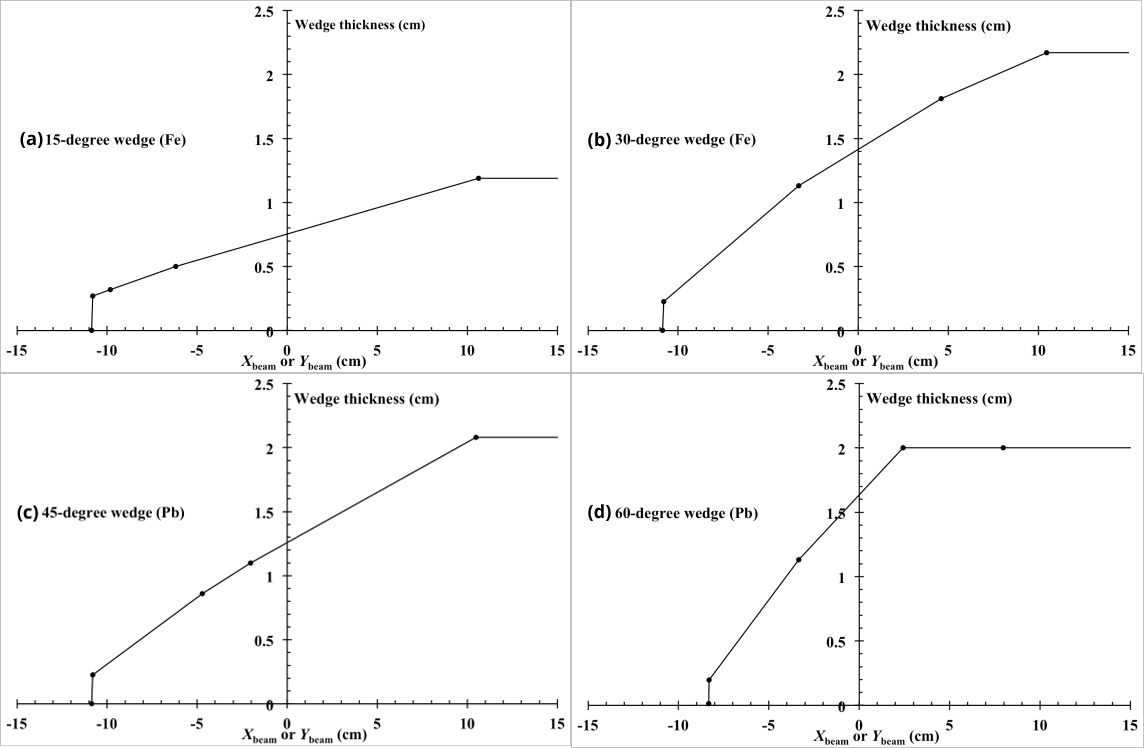
The 15° and 30° wedge filters are made of proprietary iron alloys, and the 45° and 60° wedge filters are made of proprietary lead alloys. Accordingly, to effectively calculate the wedge-filtered dose, we introduced a factor, called ρwedge_factor, giving the ratio of the mass density of the wedge material to that of pure iron or lead (assuming, to a first approximation, that the wedge material is composed of iron or lead, though its density is different from the density of pure iron or lead) for each of the four wedges. We set ρwedge_factor = 0.900 for the 15° wedge; ρwedge_factor = 0.915 for the 30° wedge; ρwedge_factor = 0.955 for the 45° wedge; and ρwedge_factor = 0.930 for the 60° wedge. These factors were obtained by comparing calculated and measured PDD and OCR datasets.
Each wedge body is attached to a 0.2 cm thick acrylic plate. Figure 14 shows cross-sectional body views of the wedges. The vertical axis shows the isocenter-axis components of the wedge thickness measured along ray lines, as a function of Xbeam or Ybeam on the isocenter plane. Each view forms a polygonal structure with corners marked by dots.
Calculation of PDD and OCR
The dose calculations in water phantoms described below were performed by setting the density of water to 0.990 g/cm3 to obtain the most accurate calculation results (this value is approximately 0.65% less than that at room temperature). We calculated the dose at a point P(Xc, Yc, Zc) in a water phantom, using a polar coordinate system (r', Φ, θ) derived from the (xv, yv, zv) coordinate system (Figure 2). Using the procedures described in Appendix B for setting steps of (Δr', ΔΦ, Δθ) and for setting the effective point for each volume element ΔV on the r'-axis, the dose calculation ability was assessed with PDD and OCR datasets that were measured in water phantoms using a 0.125 cm3 ionization chamber (dimension of sensitive volume: radius 2.75 mm, length 6.5 mm; PTW 31002, Radiation Products Design, Inc.), setting the effective center of the chamber to coincide with each measuring point.
Setting the source–surface distance (SSD) to be 100 cm (equal to the source–axis distance (SAD)), we let the PDD be defined along the isocenter axis (Xbeam = Ybeam = 0 cm) as:
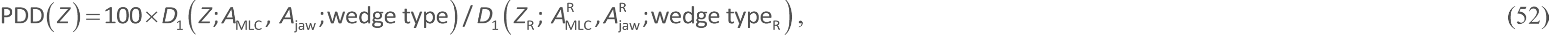
where D1 in the numerator is the dose at a phantom at depth Z on the isocenter axis for an MLC field (AMLC) under a jaw field (Ajaw) with no wedge used (wedge type = 0) or with one of the four wedges (wedge type = 1-4, also indicating its insertion direction); and D1 in the denominator is the reference dose at a phantom at a reference depth of ZR = 10 cm on the isocenter axis under a reference jaw field of ![]() with no MLC (namely,
with no MLC (namely, ![]() , an infinite field) and with no wedge (wedge typeR = 0), where the symbol is used below as the reference dose.
, an infinite field) and with no wedge (wedge typeR = 0), where the symbol is used below as the reference dose.
Next, setting the source–chamber distance (SCD) to be 100 cm (= SAD), we let the OCR be defined at a point (Xbeam, Ybeam) on the isocenter plane (Zbeam = 0 cm) as:
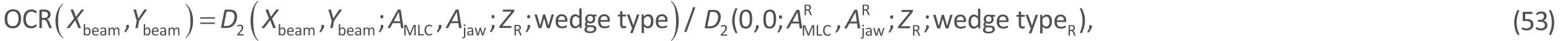
where D2 in the numerator is the dose at a point (Xbeam, Ybeam) on the isocenter plane at a reference depth of ZR on the isocenter axis for an MLC field (AMLC) under a jaw field (Ajaw) with no wedge filter (wedge type = 0) or with one of the four wedges (wedge type = 1-4) also indicating its insertion direction); and D2 in the denominator is the reference dose at the isocenter point on the isocenter plane at the reference depth (ZR) under a reference jaw field of ![]() with no MLC (namely,
with no MLC (namely, ![]() and with no wedge (wedge typeR = 0), where the symbol
and with no wedge (wedge typeR = 0), where the symbol ![]() is used below as the reference dose.
is used below as the reference dose.
According to the section of Dose calculation principle, each of D1 and D2 in equations 52 and 53 is typically composed of the nine dose components ![]() or the three dose components (Dprim, Dscat and Dcont).
or the three dose components (Dprim, Dscat and Dcont).
Experimental studies and discussionTop
The PDD and OCR datasets in the water phantoms were calculated and measured, where the square AMLC and Ajaw fields used below were all symmetric with respect to the Xbeam and Ybeam axes. It should be noted that, for any given square AMLC field, the MLC leaves not taking part in forming the open AMLC field were intentionally closed at Ybeam = 0 cm, and that each of the measured PDD or OCR datasets (drawn in dots in the figures below), producing the ratio of the dose relative to the reference dose, had a relative error of approximately ±0.7% because each measurement of D1 and D2 at a fixed point had a relative error of approximately ±0.5%.
PDD datasets
The calculated and measured PDD (PDDcalc and PDDmeas) datasets, given as a function of the depth (Z) of a phantom on the isocenter axis under each irradiation condition, are shown below. Let the PDDcalc components corresponding to the nine dose components mentioned above be expressed as:
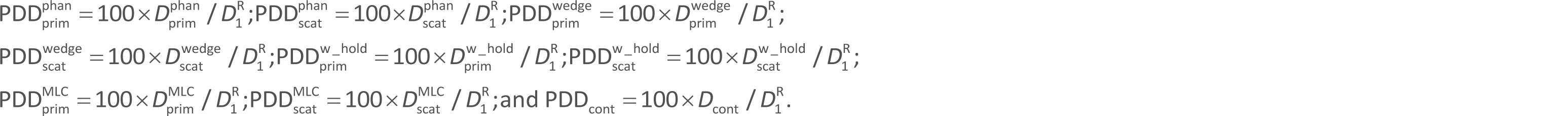
Then we have:

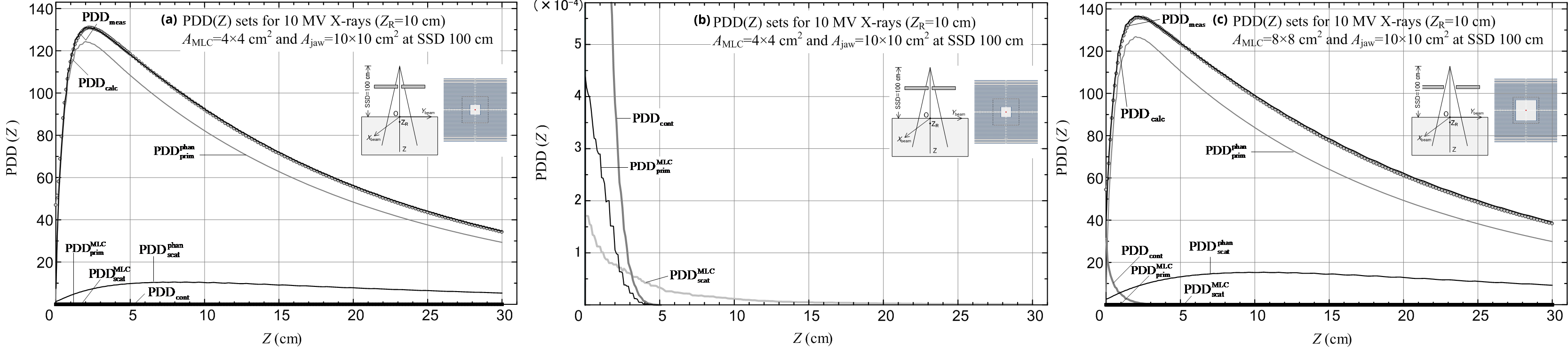
First, PDD(Z) datasets with no wedge used were calculated and measured for combinations of square AMLC and Ajaw fields. We set MLC fields of AMLC = 4 × 4-10 × 10 cm2 for a jaw field of Ajaw = 10 × 10 cm2; we set MLC fields of AMLC = 4 × 4-15 × 15 cm2 for a jaw field of Ajaw = 15 × 15 cm2; and we set MLC fields of AMLC = 4 × 4-20 × 20 cm2 for a jaw field of Ajaw = 20 × 20 cm2. Figures 15a-c show the PDDcalc (including its components) and PDDmeas datasets: diagram (a) is for a combination of AMLC = 4 × 4 cm2 and Ajaw = 10 × 10 cm2 (details of the lower dose components are shown in diagram (b)); and diagram (c) is for a combination of AMLC = 8 × 8 cm2 and Ajaw = 10 × 10 cm2 fields. It can be seen that (a) each of the primary and scatter doses from the MLC can be ignored; (b) the electron contamination dose decreases as the AMLC field decreases for a given Ajaw field; and (c) the calculated data at depths greater than around 20 cm are approximately 1–2% greater than the corresponding measured data (this paper does not analyze further why such large deviations were produced); and (d) ![]() and PDDcont = 0 at depths greater than approximately 5.8 cm. Results with almost the same calculation accuracy were also obtained for the other combinations of AMLC and Ajaw fields.
and PDDcont = 0 at depths greater than approximately 5.8 cm. Results with almost the same calculation accuracy were also obtained for the other combinations of AMLC and Ajaw fields.
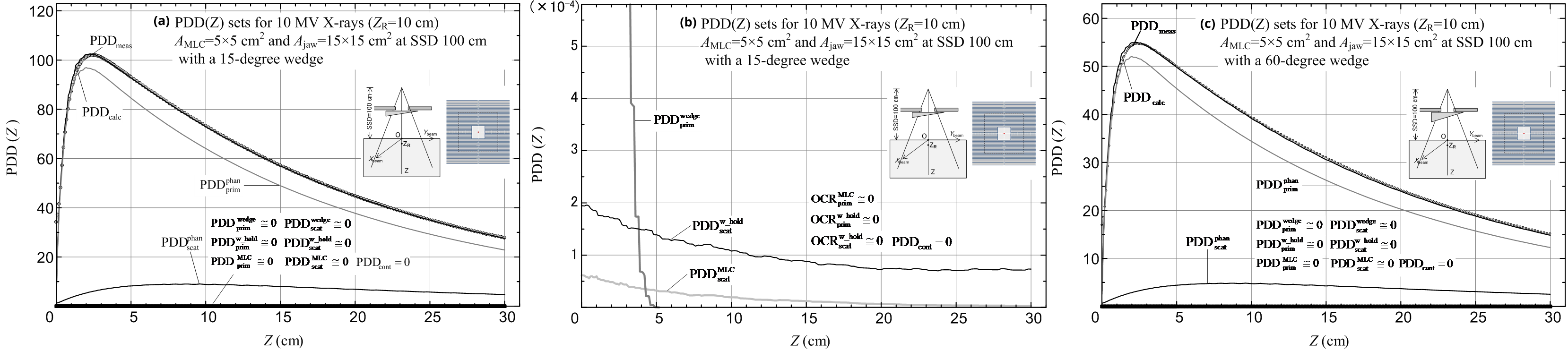
Second, PDD(Z) datasets using the 15°, 30°, 45° and 60° wedges in the direction of the Ybeam axis were calculated and measured for combinations of square AMLC and Ajaw fields as follows: we set AMLC = 4 × 4 - 10 × 10 cm2 for a jaw field of Ajaw = 10 × 10 cm2; we set AMLC = 4 × 4-15 × 15 cm2 for a jaw field of Ajaw = 15 × 15 cm2; and we set AMLC = 4 × 4-20 × 20cm2 for a jaw field of Ajaw = 20 × 20 cm2 (excluding the case where the 60° wedge is used). Figures 16a-c show the PDDcalc (including its components) and PDDmeas datasets for a combination of AMLC = 5 × 5 cm2 and Ajaw = 15 × 15 cm2 fields: diagram (a) is for the 15° wedge (details of the lower dose components are shown in diagram (b)); and diagram (c) is for the 60° wedge. It can be seen that the electron contamination dose virtually vanishes with the use of each of the wedges (namely, PDDcont = 0), and that each of the primary and scatter doses from the wedge and MLC can be ignored (namely, ![]() where
where ![]() at depths greater than approximately 5.6 cm). The calculation results in the buildup region are relatively poor (Figure 16a shows deviations = -28.2% (Z = 0.008 cm) to 6.8% (Z = 0.8 cm), and Figure 16c shows deviations = -80.7% (Z = 0.008 cm) to 8.2% (Z = 0.8 cm); this paper does not analyze further why such large deviations were produced), although the calculation results at depths beyond the buildup region are relatively accurate (Figure 16a shows deviations = -0.6% (Z = 10.2 cm) to 0.3% (Z = 2.6 cm), and Figure 16c shows deviations = -2% (Z = 30 cm) to 0.5% (Z = 2.5 cm). Results with almost the same calculation accuracy were also obtained for the other PDD datasets.
at depths greater than approximately 5.6 cm). The calculation results in the buildup region are relatively poor (Figure 16a shows deviations = -28.2% (Z = 0.008 cm) to 6.8% (Z = 0.8 cm), and Figure 16c shows deviations = -80.7% (Z = 0.008 cm) to 8.2% (Z = 0.8 cm); this paper does not analyze further why such large deviations were produced), although the calculation results at depths beyond the buildup region are relatively accurate (Figure 16a shows deviations = -0.6% (Z = 10.2 cm) to 0.3% (Z = 2.6 cm), and Figure 16c shows deviations = -2% (Z = 30 cm) to 0.5% (Z = 2.5 cm). Results with almost the same calculation accuracy were also obtained for the other PDD datasets.
OCR datasets
This section presents details of the calculated and measured OCR (OCRcalc and OCRmeas) datasets, with the Ybeam value varied and Xbeam kept constant, or with the Xbeam value varied and Ybeam kept constant, on the isocenter plane at the reference depth (ZR) under each irradiation condition. Let the OCRcalc components corresponding to the nine dose components mentioned above be expressed as:
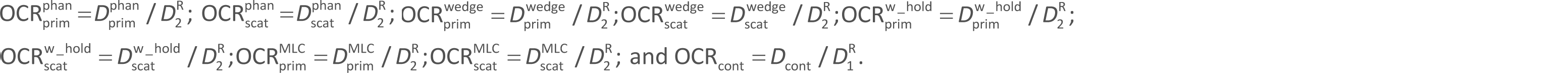
Then we have:
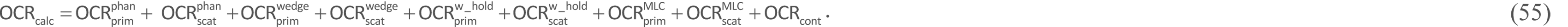
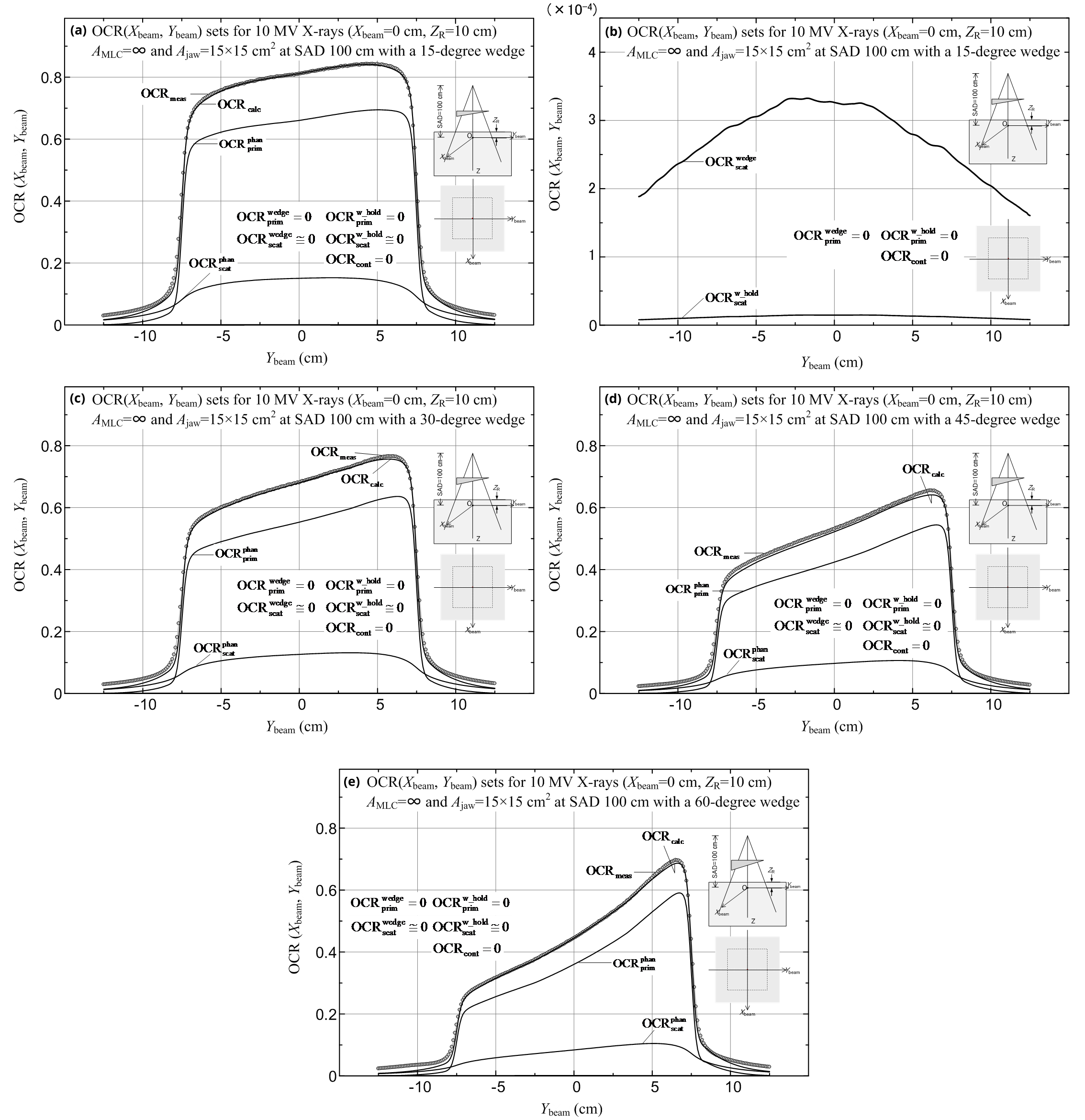
First, we calculated and measured the OCR(Xbeam, Ybeam) datasets, with the Ybeam value varied and Xbeam = 0 cm on the isocenter plane at a reference depth of ZR = 10 cm, setting each of the four wedges in the direction of the Ybeam axis and with no MLC (AMLC = ∞). When using the 15°, 30° and 45° wedges, we set square jaw fields of Ajaw = 5 × 5 - 20 × 20 cm2. When using the 60° wedge, we set square jaw fields of Ajaw = 5 × 5 - 15 × 15 cm2. Figures 17a-e show the OCRcalc (including its components) and OCRmeas datasets for a jaw field of Ajaw = 15 × 15 cm2: diagram (a) is for the 15° wedge (details of the lower dose components are shown in diagram (b)); diagram (c) is for the 30° wedge; diagram (d) is for the 45° wedge; and diagram (e) is for the 60° wedge. We obtain ![]() and
and ![]() at points around Ybeam = 0 cm. For all the calculation points, we obtain OCRcont = 0,
at points around Ybeam = 0 cm. For all the calculation points, we obtain OCRcont = 0, ![]() and
and ![]() (because the contaminant electrons and the secondary electrons from the wedge device are all shielded by the wedge and the 10 cm of water). In general, both the OCRcalc and OCRmeas datasets were in good agreement (with deviations of -0.03 to 0.09% at points around Ybeam = 0 cm), except in the case of Figure 17d with a relatively large deviation of -1.5% at points around Ybeam = 0 cm (this paper does not analyze further why such large deviations were produced). Results with almost the same calculation accuracy were also obtained for the other OCR datasets.
(because the contaminant electrons and the secondary electrons from the wedge device are all shielded by the wedge and the 10 cm of water). In general, both the OCRcalc and OCRmeas datasets were in good agreement (with deviations of -0.03 to 0.09% at points around Ybeam = 0 cm), except in the case of Figure 17d with a relatively large deviation of -1.5% at points around Ybeam = 0 cm (this paper does not analyze further why such large deviations were produced). Results with almost the same calculation accuracy were also obtained for the other OCR datasets.
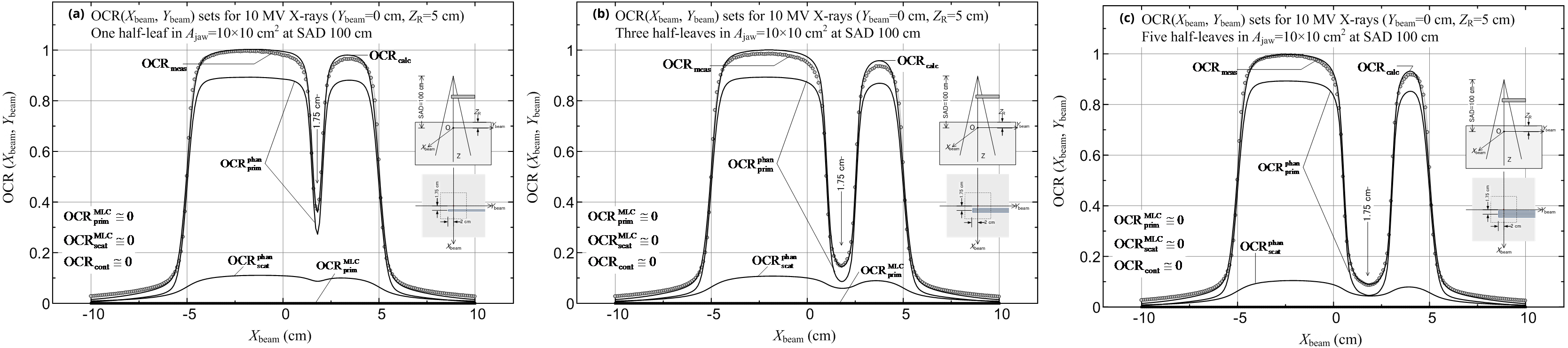
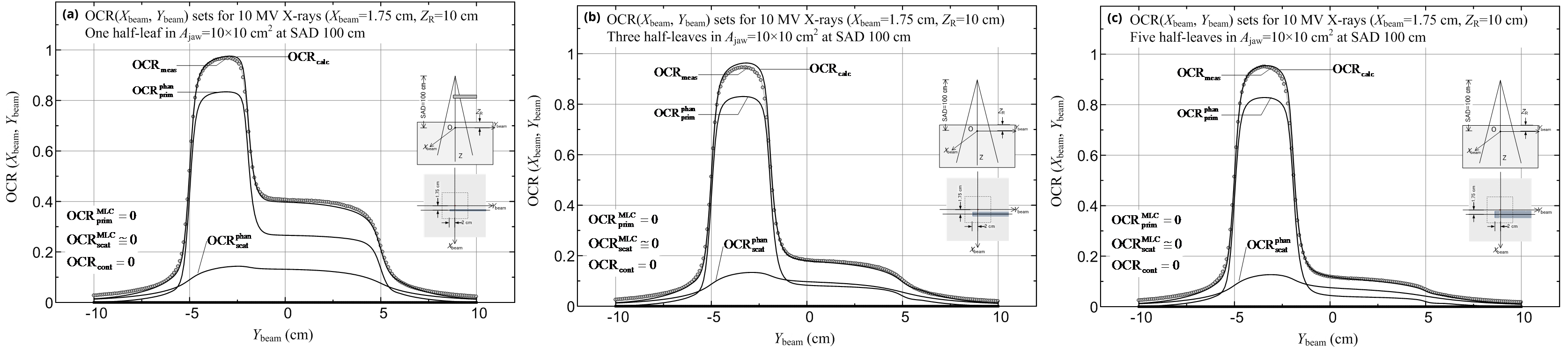
Next, we calculated and measured the OCR(Xbeam, Ybeam) datasets, with the Xbeam value varied and Ybeam = 0 cm on the isocenter plane at each reference depth of ZR = 2.5, 5 and 10 cm with no wedge used by setting each of the following three MLC leaf-blocked sections within a jaw field of Ajaw = 10 × 10 cm2. Figures 10a-c show the OCRcalc (including its components) and OCRmeas datasets for ZR = 5 cm with the use of MLC leaf-blocked sections: diagram (a) is for one half-leaf (0.5 cm in width); diagram (b) is for three consecutive half-leaves (1.5 cm in width); and diagram (c) is for five consecutive half-leaves (2.5 cm in width). For all the calculation points, we obtained OCRcont ≅ 0 (because the contaminant electrons are practically shielded by the 5 cm thick water layer), and also obtained ![]() and
and ![]() . It can be seen that the OCRmeas data behind the MLC leaf-blocked section by the one half-leaf (Figure 10a) are slightly greater (2.5%) than the OCRcalc data because the chamber readings are somewhat influenced by higher doses in the non-leaf-blocked regions, and that, in the non-leaf-blocked regions, the OCRcalc data are around 2% greater than the OCRmeas data (these large deviations may be due to the assumption that OCRsource is a function of only the off-axis distance (R0); in fact, the basic OCRsource dataset was produced based only on in-air dose data measured at points where Ybeam ≥ 0 on the Ybeam axis). Almost the same calculation accuracy was also observed for the other datasets. It should be emphasized that the work of the
. It can be seen that the OCRmeas data behind the MLC leaf-blocked section by the one half-leaf (Figure 10a) are slightly greater (2.5%) than the OCRcalc data because the chamber readings are somewhat influenced by higher doses in the non-leaf-blocked regions, and that, in the non-leaf-blocked regions, the OCRcalc data are around 2% greater than the OCRmeas data (these large deviations may be due to the assumption that OCRsource is a function of only the off-axis distance (R0); in fact, the basic OCRsource dataset was produced based only on in-air dose data measured at points where Ybeam ≥ 0 on the Ybeam axis). Almost the same calculation accuracy was also observed for the other datasets. It should be emphasized that the work of the ![]() factor (equation 47) becomes remarkable as the width of an MLC leaf-blocked section in a jaw field becomes narrow. The same statement can also be referred to the cases of Figures 11a-c described in the next place.
factor (equation 47) becomes remarkable as the width of an MLC leaf-blocked section in a jaw field becomes narrow. The same statement can also be referred to the cases of Figures 11a-c described in the next place.
Next, we calculated and measured the OCR(Xbeam, Ybeam) datasets with the Ybeam value varied and Xbeam = 1.75 cm on the isocenter plane at each reference depth of ZR = 2.5, 5 and 10 cm with no wedge used by setting each of the following three MLC leaf-blocked sections in a jaw field of Ajaw = 10 × 10 cm2. Figures 11a-c show the OCRcalc (including its components) and OCRmeas datasets for Xbeam = 1.75 cm and ZR = 10 cm: diagram (a) is for one half-leaf (0.5 cm); diagram (b) is for three consecutive half-leaves (1.5 cm); and diagram (c) is for five consecutive half-leaves (2.5 cm). For all the calculation points, we obtained OCRcont = 0 (because the contaminant electrons are practically all shielded by the 10 cm of water), and also obtained ![]() and
and ![]() . The OCRmeas data behind the MLC leaf-blocked section by the one half-leaf (Figure 11a) are slightly greater (3.5%) than the OCRcalc data because the chamber readings are also influenced by higher doses in the non-leaf-blocked regions. In Figure 11b, the OCRcalc data in the non-leaf-blocked region are around 2% greater than the OCRmeas data (this paper does not analyze further why such large deviations were produced). Figures 11a-c reveal that certain amounts of radiation leak at points which are behind the MLC leaf-blocked sections but within the jaw field. Results with almost the same calculation accuracy were also observed for the other datasets.
. The OCRmeas data behind the MLC leaf-blocked section by the one half-leaf (Figure 11a) are slightly greater (3.5%) than the OCRcalc data because the chamber readings are also influenced by higher doses in the non-leaf-blocked regions. In Figure 11b, the OCRcalc data in the non-leaf-blocked region are around 2% greater than the OCRmeas data (this paper does not analyze further why such large deviations were produced). Figures 11a-c reveal that certain amounts of radiation leak at points which are behind the MLC leaf-blocked sections but within the jaw field. Results with almost the same calculation accuracy were also observed for the other datasets.
Next, we calculated and measured the OCR(Xbeam, Ybeam) datasets, with the Ybeam value varied and Xbeam = 0, 1.25 and 3.75 cm on the isocenter plane at each reference depth of ZR = 2.5, 5 and 10 cm with the use of each of the four wedges in the direction of the Ybeam axis. For each of the 15°, 30° and 45° wedges, we set an MLC field of AMLC = 5 × 5 cm2 for the jaw fields of Ajaw = 10 × 10, 15 × 15 and 20 × 20 cm2. For the use of the 60° wedge, we set an MLC field of AMLC = 5 × 5 cm2 for the jaw fields of Ajaw = 10 × 10 and 15 × 15 cm2. Figures 18a-e show the OCRcalc (including its components) and OCRmeas datasets for Xbeam = 0 cm and ZR = 10 cm with a combination of AMLC = 5 × 5 cm2 and Ajaw = 15 × 15 cm2 fields: diagram (a) is for the 15° wedge (details of the lower dose region are shown in diagram (b)); diagram (c) is for the 30° wedge; diagram (d) is for the 45° wedge; and diagram (e) is for the 60° wedge. For all the calculation points, we obtained OCRcont = 0, ![]() ,
, ![]() and
and ![]() (because the contaminant electrons and the secondary electrons from the MLC and wedge devices cannot reach each of the calculation points), and also obtained
(because the contaminant electrons and the secondary electrons from the MLC and wedge devices cannot reach each of the calculation points), and also obtained ![]() and
and ![]() . We obtained
. We obtained ![]() at points around Ybeam = 0. Figures 18a, c-e show that the deviations of the OCRcalc data at Ybeam = 0 cm are -0.8%, -1.8%, -1.1% and -1.8%, respectively (these deviations may be caused by the inaccurate estimates of ρwedge_factor given for the wedges under the given OCRsource distribution), and that certain amounts of X-rays leak at points which are outside the MLC field but within the jaw field. Similar results were also observed in other irradiation cases, as described below. Results with almost the same calculation accuracy were also obtained for the other OCR datasets.
at points around Ybeam = 0. Figures 18a, c-e show that the deviations of the OCRcalc data at Ybeam = 0 cm are -0.8%, -1.8%, -1.1% and -1.8%, respectively (these deviations may be caused by the inaccurate estimates of ρwedge_factor given for the wedges under the given OCRsource distribution), and that certain amounts of X-rays leak at points which are outside the MLC field but within the jaw field. Similar results were also observed in other irradiation cases, as described below. Results with almost the same calculation accuracy were also obtained for the other OCR datasets.
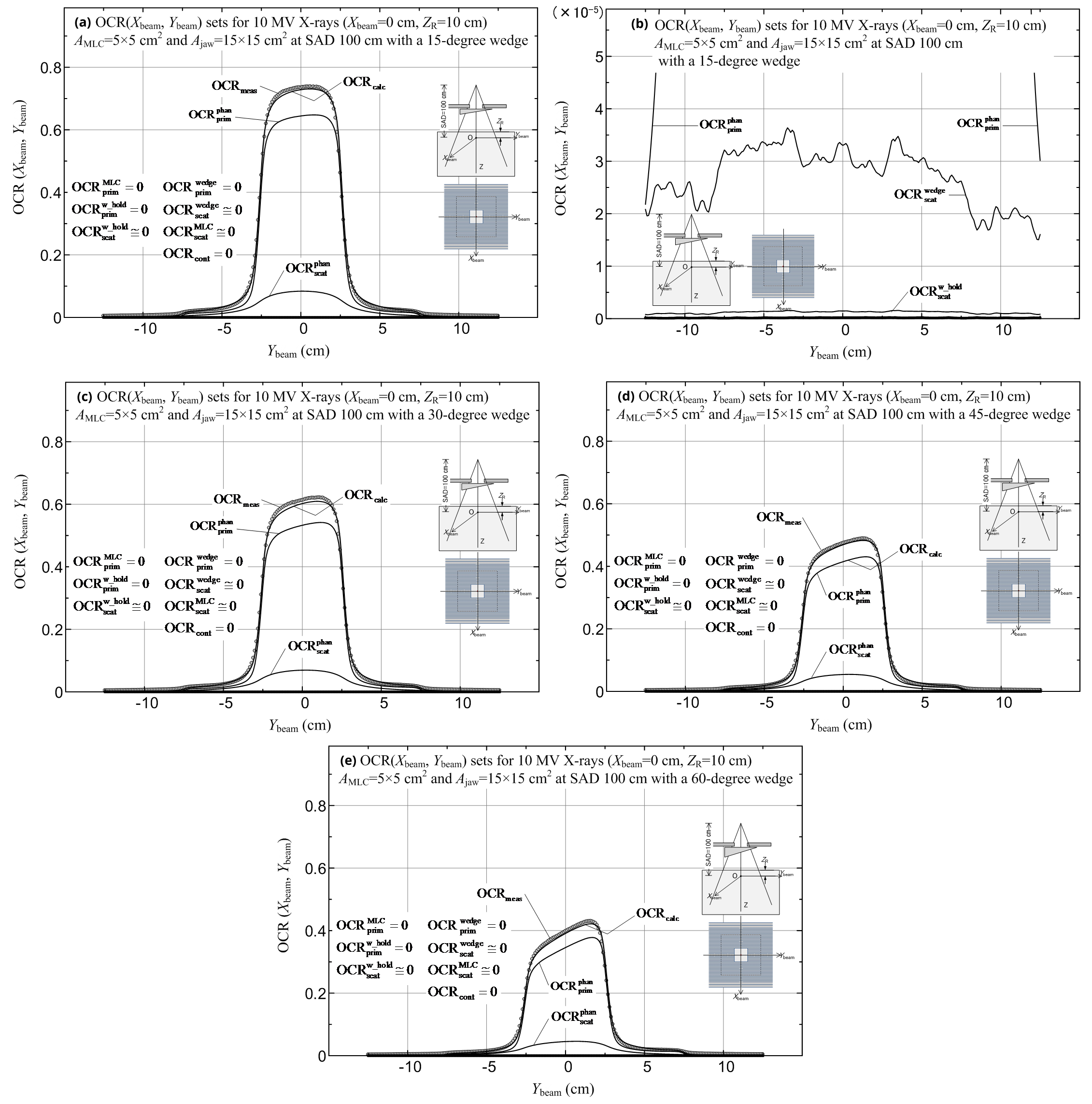
Next, we calculated and measured the OCR(Xbeam, Ybeam) datasets, with the Ybeam value varied and Xbeam = 0, 1.25 and 3.75 cm on the isocenter plane at each reference depth of ZR = 2.5, 5 and 10 cm using each of the four wedges in the direction of the Ybeam. When using the 15°, 30° and 45° wedges, we set square jaw fields of Ajaw = 5 × 5 - 20 × 20 cm2. When using the 60° wedge, we set square jaw fields of Ajaw = 5 × 5 - 15 × 15 cm2. Figures 19a-c show the OCRcalc (including its components) and OCRmeas datasets for ZR = 10 cm, with the use of the 45° wedge for a combination of AMLC = 5 × 5 cm2 and Ajaw = 15 × 15 cm2 fields: diagram (a) is for Xbeam = 0 cm; diagram (b) is for Xbeam = 1.25 cm; and diagram (c) is for Xbeam = 3.75 cm. For all the calculation points, we obtained OCRcont = 0 (because the contaminant electrons are all shielded by the wedge and the 10 cm thick water layer), and also obtained ![]() ,
, ![]() and
and ![]() (because the secondary electrons from the MLC and wedge devices cannot reach each of the calculation points). We obtained
(because the secondary electrons from the MLC and wedge devices cannot reach each of the calculation points). We obtained ![]() ,
, ![]() and
and ![]() at points around Ybeam = 0 cm. The OCRcalc deviations at Ybeam = 0 cm are -1.1% in Figure 19a and -1.9% in Figure 19b (these deviations may also be caused by the inaccurate estimate of ρwedge_factor given for the wedge under the given OCRsource distribution). Figure 19c similarly shows the results for Xbeam = 3.75 cm outside the AMLC field, illustrating the sharp changes in dose distribution near the point of Ybeam = 0 cm (due to the large X-ray leakage from the closed parts, where the pairs of A- and B-MLC leaves are just closed). It also demonstrates that the OCRmeas data are smaller than the OCRcalc data at points around Ybeam = 0 cm, because the measurements by the chamber reflect the lower doses in the MLC-shielded region. Figures 19a-c show that certain amounts of X-rays leak at points which are outside the MLC field but within the jaw field. Almost the same calculation accuracy was also observed for the other OCR datasets.
at points around Ybeam = 0 cm. The OCRcalc deviations at Ybeam = 0 cm are -1.1% in Figure 19a and -1.9% in Figure 19b (these deviations may also be caused by the inaccurate estimate of ρwedge_factor given for the wedge under the given OCRsource distribution). Figure 19c similarly shows the results for Xbeam = 3.75 cm outside the AMLC field, illustrating the sharp changes in dose distribution near the point of Ybeam = 0 cm (due to the large X-ray leakage from the closed parts, where the pairs of A- and B-MLC leaves are just closed). It also demonstrates that the OCRmeas data are smaller than the OCRcalc data at points around Ybeam = 0 cm, because the measurements by the chamber reflect the lower doses in the MLC-shielded region. Figures 19a-c show that certain amounts of X-rays leak at points which are outside the MLC field but within the jaw field. Almost the same calculation accuracy was also observed for the other OCR datasets.
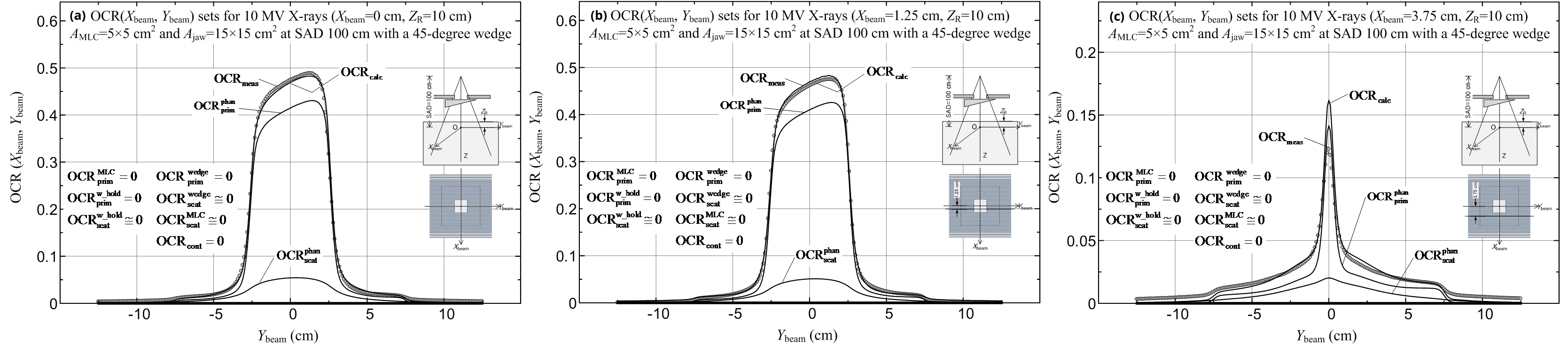
Finally, we calculated and measured the OCR(Xbeam, Ybeam) datasets, with the Xbeam value varied and Ybeam = 0, -1.25 and -3.75 cm on the isocenter plane at each reference depth of ZR = 2.5, 5 and 10 cm, using the four wedges in the direction of the Xbeam axis. When using the 15°, 30° and 45° wedges, we set square jaw fields of Ajaw = 5 × 5 - 20 × 20 cm2 for an MLC field of AMLC = 5 × 5 cm2. When using the 60° wedge, we set square jaw fields of Ajaw = 5 × 5 - 15 × 15 cm2 for an MLC field of AMLC = 5 × 5 cm2. Figures 20a-c show the OCRcalc (including its components) and OCRmeas datasets for ZR = 10 cm with the use of the 45° wedge for a combination of AMLC = 5 × 5 cm2 and Ajaw = 15 × 15 cm2 fields: diagram (a) is for Ybeam = 0 cm; diagram (b) is for Ybeam = -1.25 cm; and diagram (c) is for Ybeam = -3.75 cm. These OCRcalc and OCRmeas results clearly indicate variations in X-ray beam attenuation along the direction of wedge insertion. With respect to each of the diagrams, we obtained OCRcont = 0, ![]() ,
, ![]() and
and ![]() for all the calculation points (because the contaminant electrons and the secondary electrons from the MLC and wedge devices cannot reach each of the calculation points); and we obtained
for all the calculation points (because the contaminant electrons and the secondary electrons from the MLC and wedge devices cannot reach each of the calculation points); and we obtained ![]() ,
, ![]() and
and ![]() near the point of Xbeam = 0 cm Figure 20a shows waveform dose distributions in the left- and right-hand regions that are outside the MLC field but within the jaw field, where the pairs of A- and B-MLC leaves are just closed. In the waveform dose distributions, the OCRmeas data are much smaller than the OCRcalc data because the measurements by the chamber of finite size reflect the lower doses in the MLC-shielded region. There are relatively large deviations in OCRcalc resulting from the measurement (OCRmeas) at Xbeam = 0 cm; Figure 20a shows -1.1%, and Figure 20b shows -1.7% (these deviations may also be caused by the inaccurate magnitude of ρwedge_factor given for the wedge under the given OCRsource distribution). Figure 20c shows the OCR datasets outside the AMLC field, illustrating waveform dose distributions outside the AMLC field but within the jaw field, with pairs of large and small waves repeated (reflecting the geometrical features of the half leaves of types 1 and 2 as shown in Figures 12 and 13, and clearly showing X-ray leakages in the corresponding region). Almost the same calculation accuracy was also observed for the other OCR datasets.
near the point of Xbeam = 0 cm Figure 20a shows waveform dose distributions in the left- and right-hand regions that are outside the MLC field but within the jaw field, where the pairs of A- and B-MLC leaves are just closed. In the waveform dose distributions, the OCRmeas data are much smaller than the OCRcalc data because the measurements by the chamber of finite size reflect the lower doses in the MLC-shielded region. There are relatively large deviations in OCRcalc resulting from the measurement (OCRmeas) at Xbeam = 0 cm; Figure 20a shows -1.1%, and Figure 20b shows -1.7% (these deviations may also be caused by the inaccurate magnitude of ρwedge_factor given for the wedge under the given OCRsource distribution). Figure 20c shows the OCR datasets outside the AMLC field, illustrating waveform dose distributions outside the AMLC field but within the jaw field, with pairs of large and small waves repeated (reflecting the geometrical features of the half leaves of types 1 and 2 as shown in Figures 12 and 13, and clearly showing X-ray leakages in the corresponding region). Almost the same calculation accuracy was also observed for the other OCR datasets.
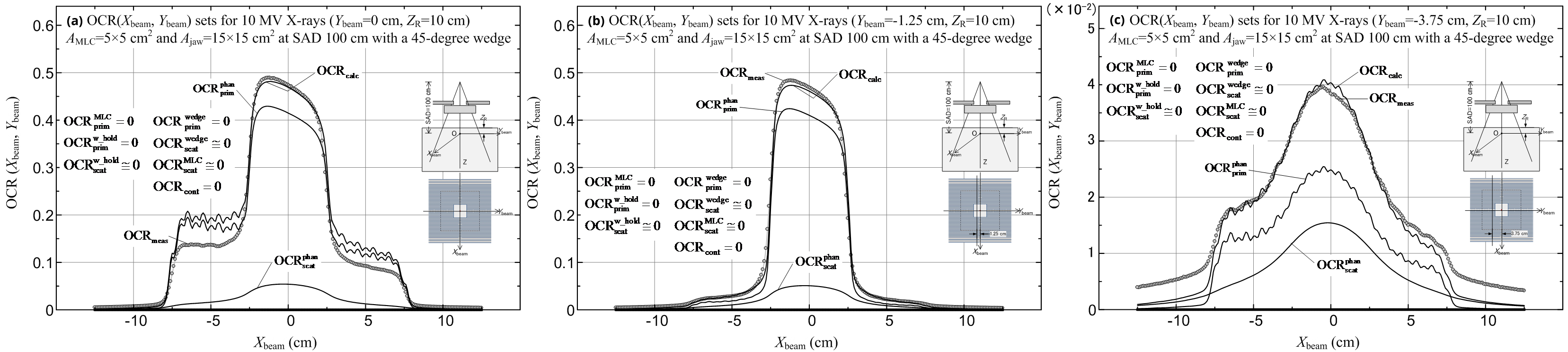
Figures 21a-d show the OCRcalc (including its components) and OCRmeas datasets for ZR = 2.5 cm with the use of the 60° wedge for a combination of AMLC = 5 × 5 cm2 and Ajaw = 15 × 15 cm2 fields: diagram (a) is for Ybeam = 0 cm (details of the lower dose region are shown in diagram (b)); diagram (c) is for Ybeam = -1.25 cm; and diagram (d) is for Ybeam = -3.75 cm. Almost the same calculation accuracy was also observed for the other OCR datasets. It should be noted that the dose leakage characteristics of the MLC are almost the same as those obtained by using a Monte Carlo simulation model [25] (Figures 20a, c and Figures 21a, d).
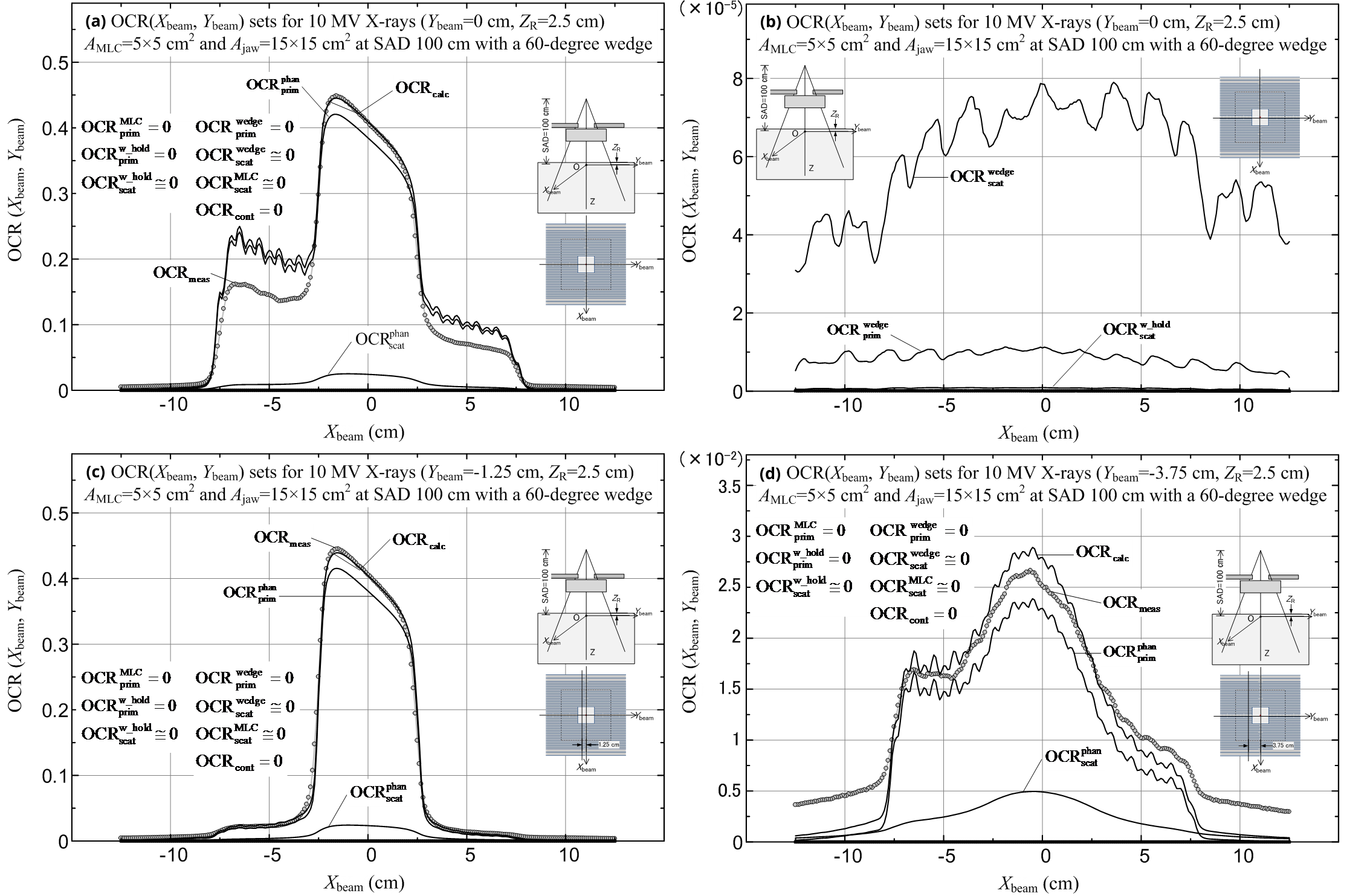
As the above-described PDD and OCR datasets show, the OCR datasets can, in general, reflect levels of dose calculation accuracy to a greater extent than the PDD datasets can. One of the most basic functions for a given linear accelerator is the OCRsource function, defined in an open infinite Ajaw field (equation 23). As the OCRsource function used in this study shows, it may not be reasonable to assume that the OCRsource function is determined only by the off-axis distance ![]() on the isocenter plane; instead, it should generally be determined by the 2D position of (X0, Y0). Moreover, the magnitude of ρwedge_factor for each wedge should be determined after acquisition of an accurate OCRsource dataset.
on the isocenter plane; instead, it should generally be determined by the 2D position of (X0, Y0). Moreover, the magnitude of ρwedge_factor for each wedge should be determined after acquisition of an accurate OCRsource dataset.
We performed theoretical and experimental studies on 10-MV X-ray dose calculations in water phantoms with multileaf collimation (MLC) and/or wedge filtration using a linear accelerator equipped with (in order from the source side) a pair of upper jaws, a pair of lower jaws, an MLC and a wedge filter. The dose calculation simulations were performed, focusing on percentage depth dose (PDD) and off-center ratio (OCR) datasets.
The dose calculations were based on a convolution method using primary and scatter dose kernels formed for energy bins of X-ray spectra reconstructed as a function of the off-axis distance. We used the MLC leaf-field output subtraction method to calculate the in-air beam intensity for points on the isocenter plane for an open MLC field under a given jaw field, employing a small, extended radiation source on the X-ray target and a large, extended radiation source on the flattening filter. The in-air beam intensity was then decomposed into each energy-bin component (EN) of the reconstructed X-ray spectra.
The 3D structures of the jaw collimator, MLC and wedge devices were replaced with 2D plates for simple dose calculation. The in-phantom dose calculation was performed by treating the phantom, the wedge, and the MLC as parts of a unified irradiated body, where we proposed to use a factor of μmed(EN) ⁄ μwater(EN) (the relative attenuation factor) for each energy-bin component (EN), instead of the relative electron density (ρe), for the medium of each volume element within the unified irradiated body, where μmed(EN) and μwater(EN) are the linear attenuation coefficients for EN photons of the volume element material and water.
ConclusionsTop
It is confirmed that, as the MLC leaf-blocked section width became narrow, the in-phantom dose calculation effect due to nonuniform incident beam intensities became great. A correction factor was then introduced for each ΔV element in the phantom. The in-phantom dose was generally separated into nine dose components: (a) the primary and scatter dose components produced in the phantom, (b) the primary and scatter dose components emanating from the MLC, (c) the primary and scatter dose components emanating from the wedge body, (d) the primary and scatter dose components emanating from the wedge holder, and (e) the contamination dose component caused by the electrons emanating from the treatment head and the air volume.
Acknowledgments
The authors are grateful to Mr. H. Mikami for his helpful advice and timely guidance throughout this study. Part of this work was performed by Yoshihisa Niioka, Takahito Chiba and Keita Masaki for their graduate studies at the Hirosaki University Graduate School of Health Sciences.
Conflicts of interest
This study was carried out in collaboration with Technology of Radiotherapy Corporation, Tokyo, Japan. This sponsor had no control over the interpretation, writing, or publication of this work.
Supplementary dataTop
ReferencesTop
[1]Ahnesjö A, Aspradakis MM. Dose calculations for external photon beams in radiotherapy. Phys Med Biol. 1999; 44(11):R99–155.Article Pubmed
[2]Ahnesjö A. Collapsed cone convolution of radiant energy for photon dose calculation in heterogeneous media. Med Phys. 1989; 16(4):577–592.Article Pubmed
[3]Iwasaki A, Kubota M, Hirota J, Fujimori A, Suzaki K, et al. Characteristic features of a high-energy X-ray spectra estimation method based on the Waggener iterative perturbation principle. Med Phys. 2006; 33(11):4056–4063.Article Pubmed
[4]Iwasaki A, Kimura S, Sutoh K, Kamimura K, Sasamori M, et al. Reconsideration of the Iwasaki–Waggener iterative perturbation method for reconstructing high-energy X-ray spectra. Radiol Phys Technol. 2012; 5(2):248−269.Article Pubmed
[5]Iwasaki A. Comments on the primary and scatter dose-spread kernels used for convolution methods. Radiat Phys Chem. 2002; 65(6):595−597.Article
[6]Iwasaki A, Kimura S, Sutoh K, Kamimura K, Sasamori M, et al. A convolution/superposition method using primary and scatter dose kernels formed for energy bins of X-ray spectra reconstructed as a function of off-axis distance: a theoretical study on 10-MV X-ray dose calculations in thorax-like phantoms. Radiol Phys Technol. 2011; 4(2):203−215.Article Pubmed
[7]Kimura S, Sutoh K, Kamimura K, Iwasaki A, Sasamori M, et al. A convolution/superposition method using primary and scatter dose kernels formed for energy bins of X-ray spectra reconstructed as a function of off-axis distance: Comparison of calculated and measured 10-MV X-ray doses in thorax-like phantoms. Radiol Phys Technol. 2011; 4(2):216−224.Article Pubmed
[8]Hubbell JH. Photon mass attenuation and energy-absorption coefficients. Int J Appl Radiat Isot. 1982; 33(11):1269−1290.Article
[9]O’Connor JE. The variation of scattered X-rays with density in an irradiated body. Phys Med Biol. 1957; 1(4):352–369.Article Pubmed
[10]Woo MK, Cunningham JR. The validity of the density scaling method in primary electron transport for photon and electron beams. Med Phys. 1990; 17(2):187–194.Article Pubmed
[11]Iwasaki A, Ishito T. The differential scatter-air ratio and differential backscatter factor method combined with the density scaling theorem. Med Phys. 1984; 11(6):755–763.Article Pubmed
[12]Miyashita H, Hatanaka S, Fujita Y, Hashimoto S, Myojyoyama A, et al. Quantitative analysis of in-air output ratio. J Radiat Res. 2013; 54(3):553−560.Article Pubmed
[13]Medina AL, Teijeiro A, Garcia J, Esperon J, Terron JA, et al. Characterization of electron contamination in megavoltage photon beams. Med Phys. 2005; 32(5):1281–1292.Article Pubmed
[14]Asuni G, Jensen JM, McCurdy BMC. A Monte Carlo investigation of contaminant electrons due to a novel in vivo transmission detector. Phys Med Biol. 2011; 56(4):1207−1223.Article Pubmed
[15]González W, Anguiano M, Lallena AM. A source model for the electron contamination of clinical linac heads in photon mode. Biomed Phys Eng Express. 2015; 1(2):025202.Article
[16]Kimura S, Iwasaki A, Sutoh K, Seino M, Komai F, et al. Calculation of MLC in-air outputs using a leaf-field output subtraction method. Proc. of the 15th Int. Conf. on the Use of Computers in Radiation Therapy. 2007; 1:425−429.
[17]Zhu TC, Bjärngard BE. Head scatter off-axis for megavoltage X-rays. Med Phys. 2003; 30(4):533−543.Article Pubmed
[18]Zhu TC, Bjärngard BE, Xiao Y, Yang CJ. Modeling the output ratio in air for megavoltage photon beams. Med Phys. 2001; 28(6):925−937.Article Pubmed
[19]Zhu TC, Bjärngard BE, Xiao Y, Bieda M. Output ratio in air for MLC shaped irregular fields. Med Phys. 2004; 31(9):2480−2490.Article Pubmed
[20]Zhu TC, Ahnesjö A, Lam KL, Li XA, Ma C-MC, et al. Report of AAPM Therapy Physics Committee Task Group 74: In-air output ratio, Sc, for megavoltage photon beams. Med Phys. 2009; 36(11):5261−5291.Article Pubmed
[21]Khan FM, Sewchand W, Lee J, Williamson JF. Revision of tissue-maximum ratio and scatter-maximum ratio concepts for cobalt 60 and higher energy X-ray beams. Med Phys. 1980; 7(3):230−237.Article Pubmed
[22]Khan FM. The physics of radiation therapy; 3rd edition. 2003.Article
[23]Boyer A, Biggs P, Galvin J, Klein E, LoSasso T, et al. Basic applications of multileaf collimators: Report of the AAPM Radiation Therapy Committee Task Group No. 50: AAPM Report No. 72 ed. Madison, USA: Medical Physics Publishing. 2001.Article
[24]van Gasteren JJM, Heukelom S, van Kleffens HJ, van der Laarse R, Venselaar JLM, et al. The determination of phantom and collimator scatter components of the output of megavoltage photon beams: Measurement of the collimator scatter part with a beam-coaxial narrow cylindrical phantom. Radiother Oncol. 1991; 20(4):250−257.Article Pubmed
[25]Heath E, Seuntjens J. Development and validation of a BEAMnrc component module for accurate Monte Carlo modelling of the Varian dynamic Millennium multileaf collimator. Phys Med Biol. 2003; 48(24):4045–4063.Article Pubmed


