Original researchOpen Access

AbstractTop

Purposes: We perform further development for our previous Gaussian-pencil-beam-model used for calculating the electron dose in water under clinical electron-beam irradiation. The main purpose is to evaluate accurately the parallel beam depth-doses at deep depths beyond about the extrapolated range (R_p) under an infinite field. Methods: Sets of parallel beam depth-doses under an infinite field were reconstructed for beams of E=6, 12, and 18 MeV in light of the electron Monte Carlo (eMC) datasets reported by Wieslander and Knöös (2006), separating the datasets into the direct electron beam and direct-plus-indirect electron beam groups. The datasets at the deep depths were then reconstructed using each factor of 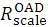. Results and conclusions: The following results were obtained by comparing the calculated datasets of depth dose (DD) and off-axis dose (OAD) with the eMC datasets: (i) The further revised Gaussian pencil beam model is of practical use without using complicated correction factors; and (ii) The DD and OAD datasets are yielded effectively over wide ranges of depths and off-axis distances.

Keywords: Gaussian pencil beam model; dose calculation; electron MC; electron beams; linear accelerator

Research highlightsTop

The dose in water caused by the clinical electron-beam irradiation is mainly composed of the doses due to the direct electrons, the indirect electrons, and the contaminant X-rays. In light of the electron Monte Carlo (eMC) datasets reported by Wieslander and Knöös (2006), this paper describes further development of the preceding Gaussian-pencil-beam-model for calculating doses in water. The main subject is how to evaluate accurately the parallel beam depth-doses at deep depths beyond about the extrapolated range (R_p) under an infinite field. Characteristic shapes were yielded effectively at shallow and deep depths for both of the depth dose curves and the off-axis dose profiles.

IntroductionTop

In 2022, we reported [1] a revised Gaussian-pencil-beam model, which was constructed on the basis of electron Monte Carlo (eMC) datasets performed by Wieslander and Knöös [2, 3] for 6-, 12-, and 18-MeV electron beams taking 10 × 10 cm² and 10 × 10/ 14 × 14 cm² applications. However, we realize that there remain two problems: (a) Parallel-beam depth-dose datasets (D_∞) at deep depths in an infinitely broad field; and (b) Characteristic shape differences of the off-axis dose (OAD) profiles at shallow and deep depths.

For resolving these problems, we use the almost same dose calculation procedures as in the previous paper, only excepting the usage purpose of the 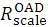factor [1] (this factor is originally introduced for recalculating reasonable OAD datasets at deep depths from ones illustrated in paper diagrams). Although this paper also utilizes a parallel-beam depth-dose dataset (D_∞) of infinite field for a given irradiation, the parallel-beam depth-dose dataset (D_∞) is partially recalculated using the 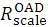factor for a point that is situated beyond about the extrapolated range (R_p). Actually, reporting this technique is the main subject of the paper.

Materials and methodsTop

Based on the depth dose (DD) and off-axis dose (OAD) datasets of the W-K eMC work [3], we similarly develop this study. Here, we would like to emphasize that each of the DD or OAD datasets is normalized with a dose of 1.0 Gy per 100 MU at the maximum dose depth (d_max) caused under the use of an open electron applicator of A_appl = 20 × 20 cm². This paper is also use the same dose unit of Gy/100 MU for each of the DD and OAD datasets.

We use KK numbers of KK=1 to 24 for the DD and OAD datasets, originally introduced in the previous paper on compiling and handling of the beam energy (E), the electron applicator (A_appl), and the utilized electron Monte Carlo (eMC). It should be noted that the eMC-based dose is separated into the dose due to (i) the direct electrons getting no interactions with the electron applicator, the dose due to (ii) the indirect electrons getting interactions with the electron applicator, and the dose due to (iii) the contaminant X-rays from within the treatment head. This paper is described only taking the direct electron beams and the direct-plus-indirect electron beams (Tables 1 and 2). The Supplementary Figure (Supp. Fig.) numbers below are the corresponding ones described in the paper of the W-K eMC work using standard and commercial eMC techniques (it should be noted that the OAD datasets for a given irradiation are yielded on two horizontal planes at shallow and deep Z_c depths).

For the direct electron beams (Table 1), the standard eMC datasets are classified into:

Under Supp. Fig. 3(a)-DD, we set KK=1 for Supp. Fig. 3(b)-OAD (Z_c=1 cm) and KK=2 for Supp. Fig. 3(c)-OAD (Z_c =5 cm);

Under Supp. Fig. 5(a)-DD, we set KK=3 for Supp. Fig. 5(b)-OAD (Z_c =2 cm) and KK=4 for Supp. Fig. 5(c)-OAD (Z_c =10 cm);

Under Supp. Fig. 3(d)-DD, we set KK=5 for Supp. Fig. 3(e)-OAD (Z_c =3 cm) and KK=6 for Supp. Fig. 3(f)-OAD (Z_c =15 cm).

Similarly, the commercial eMC datasets are classified into:

Under Supp. Fig. 3(a)-DD, we set KK=7 for Supp. Fig. 3(b)-OAD (Z_c =1 cm) and KK=8 for Supp. Fig. 3(c)-OAD (Z_c =5 cm);

Under Supp. Fig. 5(a)-DD, we set KK=9 for Supp. Fig. 5(b)-OAD (Z_c =2 cm) and KK=10 for Supp. Fig. 5(c)-OAD (Z_c =10 cm);

Under Supp. Fig. 3(d)-DD,we set KK=11 for Supp. Fig. 3(e)-OAD (Z_c =3 cm) and KK=12 for Supp. Fig. 3(f)-OAD (Z_c =15 cm).

Table 1 Values of the constants used in equation 1 for the direct electron beams (the KK numbers are the same as in the previous paper [1]).

For direct electron beams		Da (Gy/100 MU)	Za (cm)	Db (Gy/100 MU)	Zb (cm)	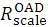(Za) (no unit)
(i) Standard eMC
	KK=1 & 2 (E=6 MeV)	1.45E-03	5	8.36E-02	3.35	0.619
	KK=3 & 4 (E=12 MeV)	3.38E-03	10	1.08E-02	6.99	39.063
	KK=5 & 6 (E=18 MeV)	5.38E-03	15	1.30E-02	9.72	36.115
(ii) Commercial eMC
	KK=7 & 8 (E=6 MeV)	1.49E-03	5	8.88E-02	3.33	1.548
	KK=9 & 10 (E=12 MeV)	3.00E-03	10	1.08E-02	7.00	34.278
	KK=11 & 12 (E=18 MeV)	5.63E-03	15	1.41E-02	9.89	50.819

For the direct-plus-indirect electron beams (Table 2), the standard eMC datasets are classified into:

Under Supp. Fig. 3(a)-DD, we set KK=13 for Supp. Fig. 3(b)-OAD (Z_c=1 cm) and KK=14 for Supp. Fig. 3(c)-OAD (Z_c =5 cm);

Under Supp. Fig. 5(a)-DD, we set KK=15 for Supp. Fig. 5(b)-OAD (Z_c =2 cm) and KK=16 for Supp. Fig. 5(c)-OAD (Z_c =10 cm);

Under Supp. Fig. 3(d)-DD, we set KK=17 for Supp. Fig. 3(e)-OAD (Z_c =3 cm) and KK=18 for Supp. Fig. 3(f)-OAD (Z_c =15 cm).

Similarly, the commercial eMC datasets are classified into:

Under Supp. Fig. 3(a)-DD, we set KK=19 for Supp. Fig. 3(b)-OAD (Z_c =1 cm) and KK=20 for Supp. Fig. 3(c)-OAD (Z_c =5 cm);

Under Supp. Fig. 5(a)-DD, we set KK=21 for Supp. Fig. 5(b)-OAD (Z_c =2 cm) and KK=22 for Supp. Fig. 5(c)-OAD (Z_c =10 cm);

Under Supp. Fig. 3(d)-DD,we set KK=23 for Supp. Fig. 3(e)-OAD (Z_c =3 cm) and KK=24 for Supp. Fig. 3(f)-OAD (Z_c =15 cm).

Table 2 Values of the constants used in equation 1 for the direct & indirect electron beams (the KK numbers are the same as in the previous paper [1]).

For direct & indirect electron beams		Da (Gy/100 MU)	Za (cm)	Db (Gy/100 MU)	Zb (cm)	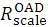(Za) (no unit)
(i) Standard eMC
	KK=13 & 14 (E = 6 MeV)	1.33E-03	5	8.96E-02	3.36	0.159
	KK=3 & 4 (E=12 MeV)	3.38E-03	10	1.08E-02	6.99	39.063
	KK=15 & 16 (E=12 MeV)	3.65E-03	10	3.01E-02	6.94	0.214
(ii) Commercial eMC
	KK=19 & 20(E=6 MeV)	1.33E-03	5	8.96E-02	3.36	0.156
	KK=21 & 22 (E=12 MeV)	3.25E-03	10	3.77E-02	6.36	0.180
	KK=23 & 24 (E=18 MeV)	5.66E-03	15	1.23E-02	9.88	1.72E+02

We propose another usage of the 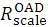factor, which is used for obtaining datasets of parallel beam depth-dose (D_∞) in an infinitely broad field using a mathematical expression as a function of depth Z in a region beyond about the extrapolated range (R_p).

For constructing such datasets of parallel beam depth-dose (D_∞), we use again the same DD datasets plotted in graphs of the paper reported by Wieslander and Knöös [3] (the construction method is the same as reported in the previous paper [1]). It has been found that, as shown later in Supp. Fig. 1, the reconstructed D_∞ datasets reported in the previous paper usually contain relatively large errors in the low-dose region at deep depths beyond about the extrapolated range (R_p). In order to avoid this situation, the previous paper performed the dose calculation introducing the 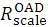factor as a dose correction factor only at each specific depth.

This paper proposes a method to reconstruct a more reasonable D_∞ dataset at deep depths for each beam irradiation. Supp. Fig. 1 shows its procedure (utilizing the DD dataset of KK=15 & 16, as illustrated below in Supp. Fig. 5b). The orange line shows a raw dataset as used in the previous paper, and the blue line shows its modified dataset proposed in the present dose calculation, setting two points along the beam axis. Let the point at Z=Z_a indicate the position of the dose (D_a) that is equal to the dose obtained using the factor of 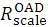as proposed in the previous paper, and let the point at Z=Z_b (<Z_a) indicate the common position of another reasonable dose of D_b estimated by eye on both dose lines. Then along the blue line for Z ≥ Z_b, we set

where α is a constant, determined by the doses of D_a and D_b, as pointed up by using yellow dots in Supp. Fig. 1, at the corresponding two positions of Z_a and Z_b.

Table 1 lists sets of (D_a, Z_a), (D_b, Z_b), and 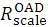(Z_a) values for KK=1-12 based on the standard or commercial eMC for the direct electron beams of E=6, 12, and 18 MeV. Similarly, Table 2 lists the corresponding datasets for KK=13-24 taking the direct and indirect electron beams. It should be noted that the Z=Z_a point is situated beyond the extrapolated range (R_p) for each irradiation [1], and that the 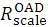factor at each Z=Z_a depth all takes much smaller or larger values than unity (we need no correction for D_a in case of 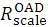=1).

We use the same dose calculation procedure as the previous one [1], only except the purpose of the usage of the 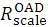factor as described above.

Supp. Fig. 2 shows how the effective square field of 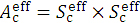at each dose calculation Z_c depth (as shaped using a square electron applicator (A_appl)) is divided equally into small sections of 40 × 40. In the previous paper [1], we has reported that the 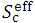function spreads exponentially with Z_c depth in water. Almost the same phenomenon is illustrated in a Monte-Carlo drawing picture on the cover of Klevenhagen’s textbook [4]. However, the perfect square-shaped fields would not be held with increasing depth in phantom like the case of the primary X-ray beam intensity distribution.

Results and discussionTop

First, we describe how the parallel-beam depth-dose datasets (D_∞) of infinite field are varied in (i) the whole Z region and (ii) the deep Z region on large scale, as follows:

Supp. Fig. 3a-c shows the direct electron beam cases on the standard eMC for (a) KK=1 & 2 (E=6 MeV), (b) KK=3 & 4 (E=12 MeV), and (c) KK=5 & 6 (E=18 MeV). Similarly, Supp. Fig. 4a-c shows the cases on the commercial eMC for (a) KK=7 & 8 (E=6 MeV), (b) KK=9 & 10 (E=12 MeV), and (c) KK=11 & 12 (E=18 MeV).

Supp. Fig. 5a-c shows the direct & indirect electron beam cases on the standard eMC for (a) KK=13 & 14 (E=6 MeV), (b) KK=15 & 16 (E=12 MeV), and (c) KK=17 & 18 (E=18 MeV). Similarly, Supp. Fig. 6a-c shows the cases on the commercial eMC for (a) KK=19 & 20 (E=6 MeV), (b) KK=21 & 22 (E=12 MeV), and (c) KK=23 & 24 (E=18 MeV).

It could be understood more clearly from the diagrams on large scale that each blue line at depths of Z ≥ Z_b is connected smoothly with the corresponding orange line at depths of Z < Z_b.

Lastly, we describe how the OAD curve pattern varies with Z_c depth by setting regions of relatively (i) shallow and (ii) deep Z_c depths, as follows:

Supp. Fig. 7a-c shows the direct electron beam cases on the standard eMC for (a) KK=1 & 2 (E=6 MeV), (b) KK=3 & 4 (E=12 MeV), and (c) KK=5 & 6 (E=18 MeV). Similarly, Supp. Fig. 8a-c shows the cases on the commercial eMC for (a) KK=7 & 8 (E=6 MeV), (b) KK=9 & 10 (E=12 MeV), and (c) KK=11 & 12 (E=18 MeV).

Supp. Fig. 9a-c shows the direct & indirect electron beam cases on the standard eMC for (a) KK=13 & 14 (E=6 MeV), (b) KK=15 & 16 (E=12 MeV), and (c) KK=17 & 18 (E=18 MeV). Similarly, Supp. Fig. 10a-c shows the cases on the commercial eMC for (a) KK=19 & 20 (E=6 MeV), (b) KK=21 & 22 (E=12 MeV), and (b) KK=23 & 24 (E=18 MeV).

It can be seen from the OAD curves that the shapes in the very shallow Z_c depths (less than ∼1E-04 cm) form triangles, the ones in the middle Z_c depths form squarish trapezoids, and the ones in the deep Zc depths form round trapezoids.

The revised Gaussian-pencil-beam-model uses a mathematical 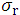expression, being reconstructed based on datasets of 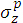for E = 6, 10, 14, and 20 MeV as reported by Bruinvis et al. [5]. On the other hand, judging from the OAD curves at very shallow depths for each of the 6, 12, and 18 MeV beam energies, we should see steep DD descents toward each zero depth. Actually, we have obtained a fact that each calculated DD curve forms zero dose values at very shallow Z_c depths (less than ∼1E-15 cm), where it should be noted that we do not use any set of parallel beam depth-doses of infinite field that descends very sharply near the zero depth, as seen from Supp. Fig. 3-6. Examining Khan’s text book [6], such dose descents are not described (details will be reported in the next article). We would like to let it be a great subject when taking inhomogeneous phantoms for dose calculations with this Gaussian-pencil-beam-model.

ConclusionTop

We conducted two supplementary studies for the previous paper: one is for the parallel-beam depth-dose dose (D_∞) at deep depths in an infinitely broad field, and the other is for the characteristic shape differences of off-axis dose (OAD) profiles at shallow and deep depths, including in the very shallow depths (less than ∼1E-04 cm). We believe that these two studies must be important for dose calculations especially when using heterogeneous phantoms or when considering the dose calculation on a cell-by-cell basis.

Acknowledgments
The authors thank Dr. Tabata for his close attention to useful suggestions for revising this paper.

Conflicts of interest
This study was carried out in collaboration with Technology of Radiotherapy Corporation, Tokyo, Japan. This sponsor had no control over the interpretation, writing, or publication of this work.

Supplementary dataTop

Supplementary material