Original researchOpen Access

AbstractTop

Purposes: We perform further development for our previous Gaussian-pencil-beam-model used for calculating the electron dose in water under clinical electron-beam irradiation. The main purpose is to evaluate accurately the parallel beam depth-doses at deep depths beyond about the extrapolated range (Rp) under an infinite field. Methods: Sets of parallel beam depth-doses under an infinite field were reconstructed for the same beams of E=6, 12, and 18 MeV in light of the electron Monte Carlo (eMC) datasets as reported by Wieslander and Knöös (2006), separating the datasets into the direct electron beam and direct-plus-indirect electron beam groups. Particularly, for each electron beam, we took serious views of the depth-dose (DD) curves near the beam entrance surface and of the OAD (off-axis dose) curves at deep depths beyond about the extrapolated range (R_p) under an infinite field. Results and conclusions: The following results were obtained by comparing the calculated DD and OAD datasets with the eMC datasets: (i) The revised Gaussian pencil beam model is of practical use without using complicated correction factors; and (ii) The DD and OAD datasets are yielded effectively over wide ranges of depths and off-axis distances, respectively.

Keywords: Gaussian pencil beam model; dose calculation; electron MC; electron beams; linear accelerator

Research highlightsTop

The dose caused by the clinical electron-beam irradiation is mainly composed of the doses due to the direct electrons, the indirect electrons, and the contaminant photons. In light of the electron Monte Carlo (eMC) datasets reported by Wieslander and Knöös (2006), the present paper describes further development of the Gaussian-pencil-beam-model for calculating doses in a homogeneous water phantom for direct electron beams and direct-plus-indirect electron beams. The study subjects are how to calculate dose-datasets accurately both near the beam entrance surface and at deep depths. Accurate datasets of depth-dose (DD) and off-axis dose (OAD) were obtained from the shallow to deep depths for each of the electron beams.

1. IntroductionTop

Wieslander and Knöös [1, 2] have reported characteristic features of the dose in homogeneous water, caused by clinical electron-beam irradiations, using an electron Monte Carlo (eMC) method for 6-, 12-, and 18-MeV electron beams by taking 10×10 cm² and 10×10/14×14 cm² applicators. The 10×10 cm² applicator is used for the 6- and 18-MeV electron beams, and the 10×10/14×14 cm2 applicator is used for the 12-MeV electron beams setting a lead plate opening of 10×10 cm² in the 14×14 cm² applicator. The dose studies are classified into three categories: (a) datasets caused by contaminant photons from the treatment head, (b) datasets caused by direct electrons that have not interacted in the electron applicator, and (c) datasets caused by indirect electrons that have interacted in the electron applicator. For each group of the 6-, 12-, and 18-MeV electron beams, the study work is performed using two eMC algorithms by setting a common virtual accelerator; one is that developed by them as the standard eMC, and the other is a commercial treatment planning system (TPS). The present paper refers to these datasets as “the W-K eMC dose datasets” or “the W-K eMC dose work.”

The eMC treatment is usually a time-consuming work. Iwasaki and others [3, 4] have reported papers to recalculate the W-K eMC dose datasets using an analytical method to shorten the treatment time. However, the reported papers have the following defects:

• Both the depth-dose (DD) datasets and the off-axis dose (OAD) datasets were inaccurately calculated in the region near the beam entrance surface by taking unreasonable calculation procedures for calculation of the factor.
• Parallel-beam depth-dose datasets (D_∞) of infinite field were not precisely estimated at deep depths beyond about the extrapolated range (R_p).
• Each set of the OAD profiles was not reconstructed by taking account of the balanced forms at deep depths.

This paper will report how these three problems are overcome for calculating doses more precisely using a mathematical analysis for a simplified homogenous water phantom, preparing future studies how to calculate doses also analytically keeping high accuracy even for heterogeneous phantoms.

MethodsTop

We describe this section based on the electron beam DD and OAD datasets of the W-K eMC dose work [2]. As described above, each of the DD and OAD datasets is yielded by setting a common virtual accelerator for both of the standard eMC and the TPS eMC. Here, it should be emphasized that each of the DD and OAD datasets is normalized with a dose of 1.0 Gy per 100 MU at the maximum dose depth (d_max) yielded by all particles of contaminant photons, direct electrons, and indirect electrons under the use of an open electron applicator of A_appl=20×20 cm². We use the same dose unit of Gy/100MU for each of the DD and OAD datasets. Here, in this paper, the “no unit” means a constant value when the factor is set exponentially and used for multiplication with the Z_c-axis in cm.

2.1. DD and OAD datasets
First, we describe how each of the electron beam DD and OAD datasets is expressed using a set of expressions for the direct electron beams and for the direct-plus-indirect electron beams. As listed in Table 1, we use the same KK numbers of KK=1 to 24 for the DD and OAD datasets published in the W-K paper of Ref. [2], as originally introduced in the previous papers [3, 4], also indicating the beam energy (E), the electron applicator (A_appl), and the standard or TPS eMC. It should be noted that each of the OAD datasets is yielded on two horizontal planes at shallow or deep Zc depth (we specify the two depths as Z₁ and Z₂, respectively), and that, although each DD dataset has no KK number directly, it is used in common with the corresponding two OAD datasets. Namely, the KK numbers also indicate the corresponding diagrams used in the W-K paper (Supp. Fig. 3a & 3b, etc.).

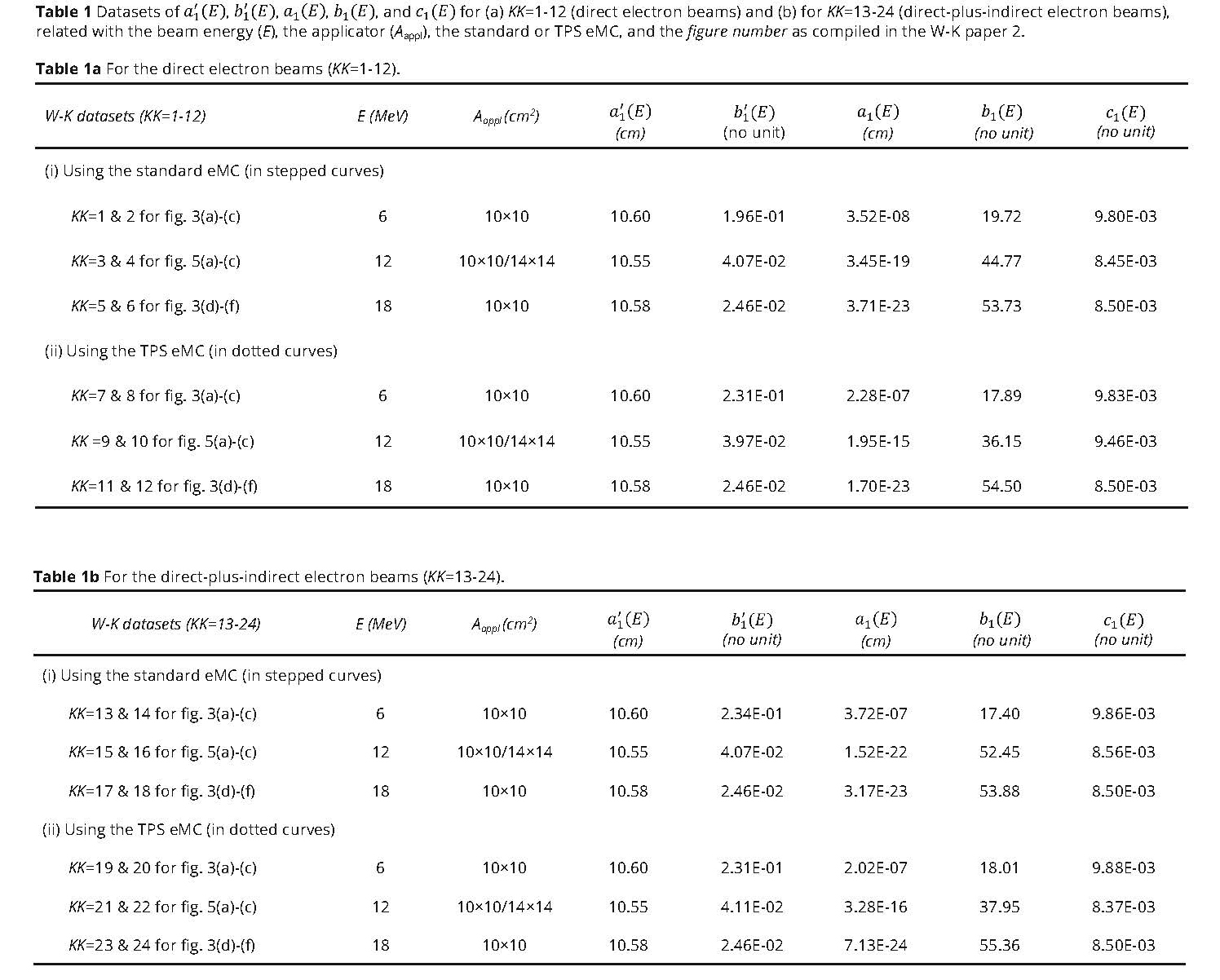
Table 1a is constructed for the direct electron beams:
(i) The standard eMC datasets are classified into:
Under the DD dataset in Supp. Fig. 3a, we set KK=1 for Supp. Fig. 3b-OAD (Z₁=1 cm) and set KK=2 for Supp. Fig. 3c-OAD (Z₂=5 cm);
Under the DD dataset in Supp. Fig. 5a, we set KK=3 for Supp. Fig. 5b-OAD (Z₁=2 cm) and set KK=4 for Supp. Fig. 5c-OAD (Z₂=10 cm);
Under the DD dataset in Supp. Fig. 3d, we set KK=5 for Supp. Fig. 3e-OAD (Z₁=3 cm) and set KK=6 for Supp. Fig. 3f-OAD (Z₂=15 cm).

(ii) The TPS eMC datasets are classified into: Under the DD dataset in Supp. Fig. 3a, we set KK=7 for Supp. Fig. 3b-OAD (Z₁=1 cm) and set KK=8 for Supp. Fig. 3c-OAD (Z₂=5 cm);
Under the DD dataset in Supp. Fig. 5a, we set KK=9 for Supp. Fig. 5b-OAD (Z₁=2 cm) and set KK=10 for Supp. Fig. 5c-OAD (Z₂=10 cm);
Under the DD dataset in Supp. Fig. 3d, we set KK=11 for Supp. Fig. 3e-OAD (Z₁=3 cm) and set KK=12 for Supp. Fig. 3f-OAD (Z₂=15 cm).

Table 1b is constructed for the direct-plus-indirect electron beams:
(i) The standard eMC datasets are classified into: Under the DD dataset in Supp. Fig. 3a, we set KK=13 for Supp. Fig. 3b-OAD (Z₁=1 cm) and set KK=14 for Supp. Fig. 3c-OAD (Z₂=5 cm);
Under the DD dataset in Supp. Fig. 5a, we set KK=15 for Supp. Fig. 5b-OAD (Z₁=2 cm) and set KK=16 for Supp. Fig. 5c-OAD (Z₂=10 cm);
Under the DD dataset in Supp. Fig. 3d, we set KK=17 for Supp. Fig. 3e-OAD (Z₁=3 cm) and set KK=18 for Supp. Fig. 3f-OAD (Z₂=15 cm).

(ii) The TPS eMC datasets are classified into:
Under the DD dataset in Supp. Fig. 3a, we set KK=19 for Supp. Fig. 3b-OAD (Z₁=1 cm) and set KK=20 for Supp. Fig. 3c-OAD (Z₂=5 cm);
Under the DD dataset in Supp. Fig. 5a, we set KK=21 for Supp. Fig. 5b-OAD (Z₁=2 cm) and set KK=22 for Supp. Fig. 5c-OAD (Z₂=10 cm);
Under the DD dataset in Supp. Fig. 3d, we set KK=23 for Supp. Fig. 3e-OAD (Z₁=3 cm) and set KK=24 for Supp. Fig. 3f-OAD (Z₂=15 cm).

2.2. Effective field side ()
In the previous papers [3, 4], we made mistakes for setting effective fields of 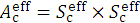at shallow depths of Z_c < Z₁. Although no large dose errors happen in the DD curves at Z_c depths beyond about 1E-05 cm for each beam energy of E=6, 12, and 18 MeV, the OAD curve forms gradually narrower widths as the Z_c depth decreases from each Z₁ depth as indicated in Ref. [4]. The present paper proposes another treatment for the 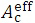field at depths of Z_c < Z₁. Here, we express the effective field side () for each beam as a function of Z_c for a given beam energy (E). We use functional expressions of (Z_c) and (Z_c, E) case by case.

For the blue lines, as illustrated in Figure 1, we set (0) on the beam entrance surface (Z_c = 0), where we simply set the value of (0) as the field side determined using the geometry of the fan beam coming out from the electron applicator by the use of the effective source-to-surface distance of SSD_eff [3]. Then we set (Z₁) for the depth of Z_c = Z₁, and set (Z₂) for the depth of Z_c = Z₂. [we can set (Z_c=0) (Z_c = Z₁) holding (Z_c = 0) 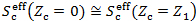]. Table 2 (composed of Tables 2a to 2d) lists datasets for both standard eMC and the TPS eMC. It should be noted that the (0) values are almost constant (10.5 or 10.6 cm) for each irradiation because of a simplified treatment for the determination (it should be noted that the brown line is used by mistake for the evaluation at depths of Z_c < Z₁ in the former papers [3, 4]).

The following expression [3, 4] has been reported for the determination of S_c^eff at depths of Z_c ≥ Z₁ using sets of a₁, b₁, and c₁ factors (see Table 1):

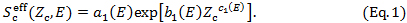
For depths of Z_c < Z₁, this paper proposes the following expression:

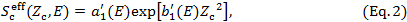
where we let 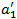(E) be equal to the (0) field side at Zc=0 determined using the above-described geometry of the fan beam coming out from the electron applicator, and then the value of 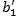(E) is determined by setting

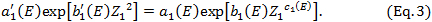
Table 1 also lists sets of 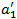(E) and 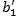(E) values for the KK numbers (this paper also uses a simplified expression of (Z_c) for (Z_c, E) in case of taking a constant beam energy E beforehand). Figure 1 shows how the effective field side () varies with depth (Z_c). 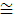As described above, Z₁ and Z₂ are specified depths used in the OAD datasets of the W-K paper (it should be emphasized that we can set (0) (Z₁); it seems that the W-K paper takes such a special Z₁ value for each beam energy (E)).

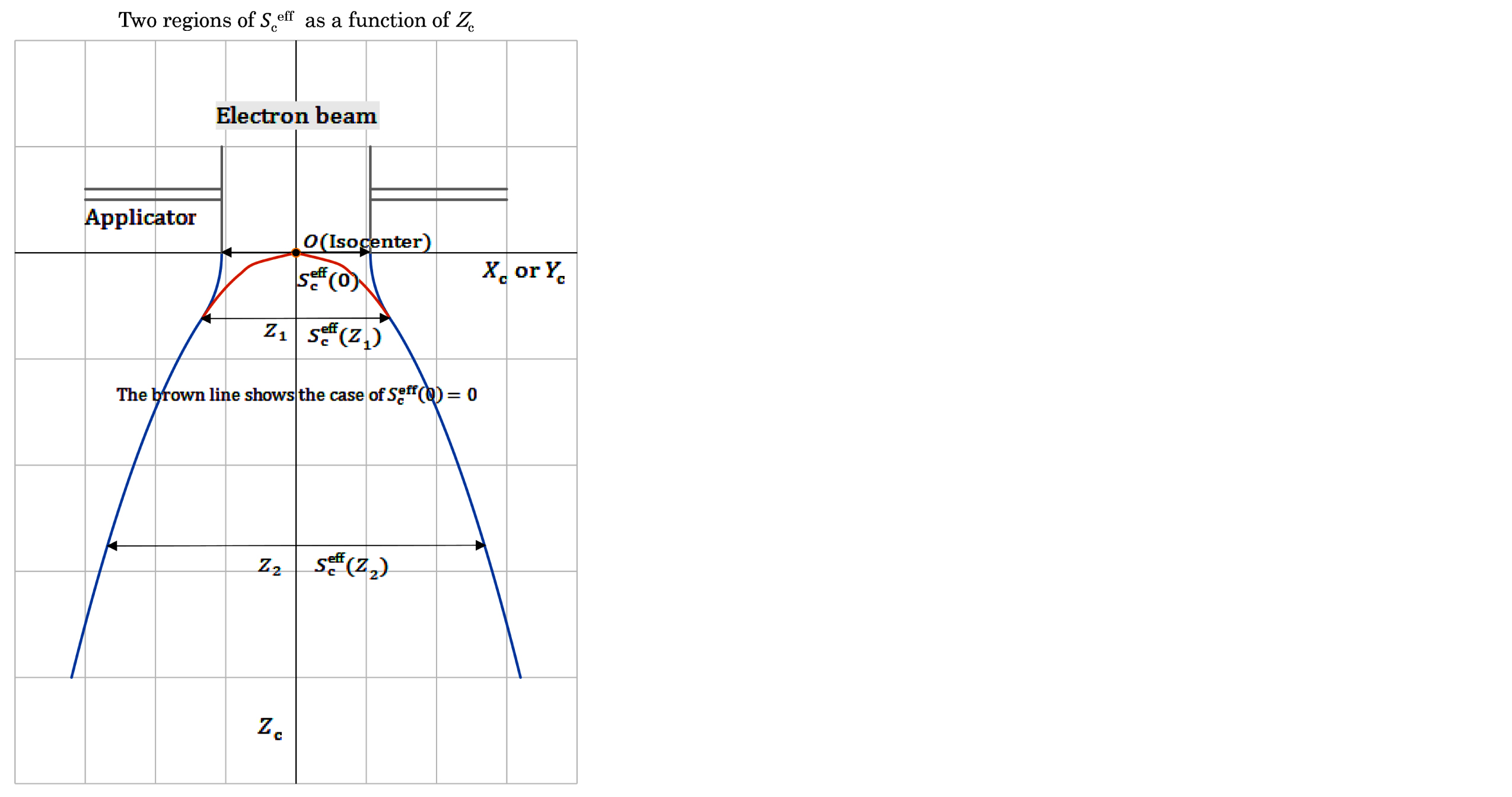
Figure 1 Two regions of as a function of Z_c. One is for Z_c < Z₁ and the other is for Z_c ≥ Z₁. The blue lines are used in this study; on the other hand, the brown line takes in the former papers by mistake, showing (0)=0.

2.3. Parallel beam depth-doses at infinite field
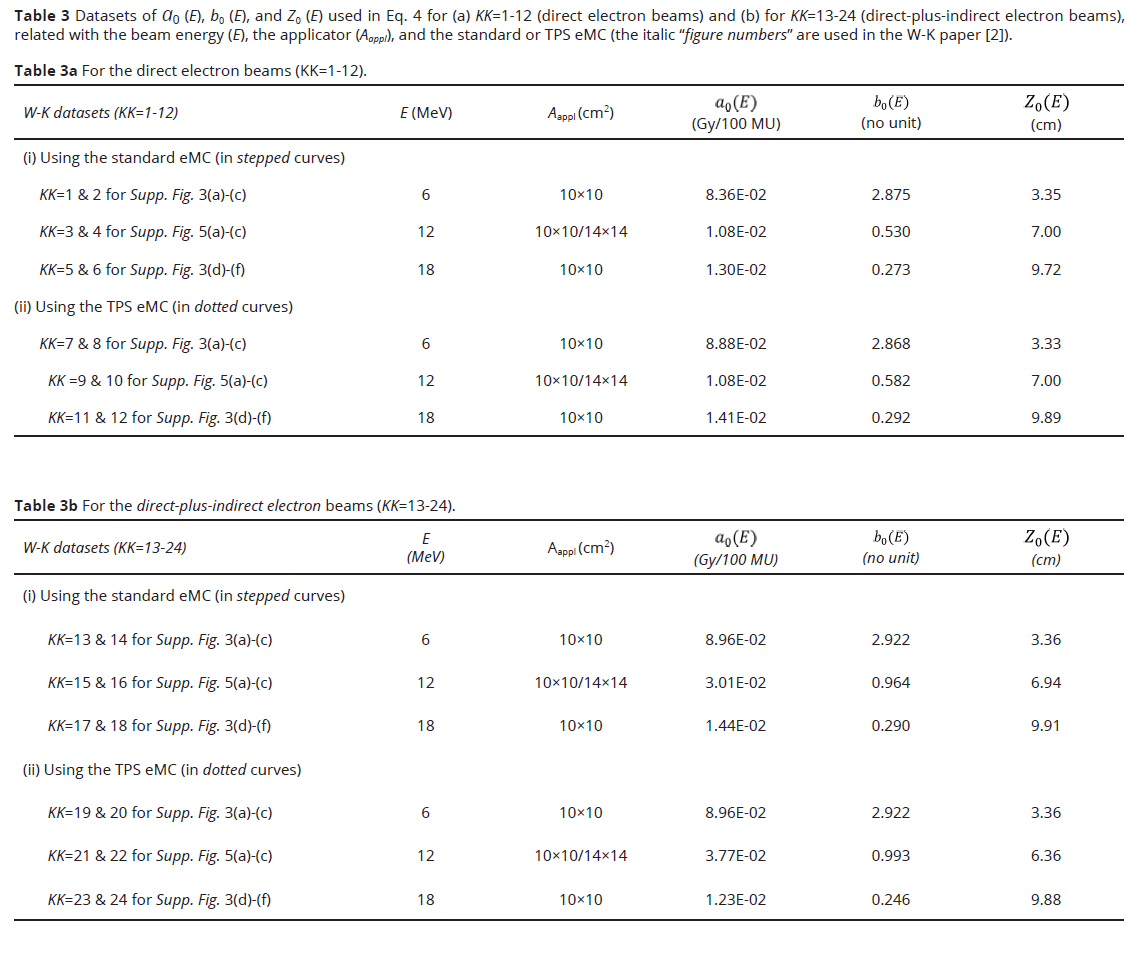
For the dose calculation for a given electron beam, the Gaussian pencil beam model uses a dataset of parallel beam depth-dose (D_∞) in an infinitely broad field. We have had experiences [3, 4] that the D_∞ datasets could reasonably be reconstructed for depths less than about the extrapolated range (R_p); however, not reasonably be reconstructed for depths beyond about the Rp range. The present paper proposes a reasonable procedure for it as follows:

Figure 2 shows a blue line expressing a raw set of D_∞ data for a given beam energy E, appearing unreasonable data at depths greater than Z_c = Z₀ (E) taking a dose of a₀ (E) at depth of Z₀ (E). Then this paper proposes a different set of D_∞ data at depths of Z_c > Z₀ (E) using a brown line as

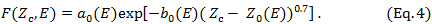
It should be noted that the constant parameter-value of 0.7 is determined by examination of sets of OAD curves produced for all the beam energies of 6, 12, and 18 MeV, and that the value of b₀ (E) is determined by examination of a set of OAD curves of E under the constant 0.7-parameter, especially by taking into account the OAD curve at the depth of Z2. Table 3 lists datasets of a₀ (E), b₀ (E), and Z₀ (E) values (a) for the direct electron beams (KK=1-12) and (b) for the direct-plus-indirect electron beams (KK=13-24).

2.4. Calculation of depth-doses for fan beams
It should be emphasized that the dose calculation for the fan beams is performed using the same procedures as in the former papers of Refs. [3 and 4], only excepting: (i) the mathematical treatment for calculation of the effective field side () for depths of Z_c < Z₁ using Eq. 2 (Figure 1); and (ii) the mathematical treatment for calculation of the parallel beam dose dataset (D_para) of infinite field at deep depths using Eq. 4 (Figure 2).

Figure 2 The blue line expresses a raw set of D_∞ data appearing unreasonable data at depths greater than Z_c = Z₀ (E) taking a dose of a₀ (E) for a given beam energy E. This paper proposes a different set of D_∞ data at depths of Z_c > Z₀ (E) using a brown line expressed by Eq. 4.

Results and discussionTop

Supplementary Figures (Supp. Fig.) 3-14 illustrate (a) & (b) DD datasets and (c) & (d) OAD datasets for E=6, 12, and 18 MeV beams, being partly compared with the corresponding dose datasets copied directly from the W-K eMC dose work (the standard or TPS eMC). For each DD or OAD dataset, we give a detailed explanation using the factors given in Figure 2 and given in Tables 1 and 2 as follows:

• Supp. Fig. 3 shows the case of the direct electron beams based on the standard eMC for each of the (a)-(d) diagrams with respect to KK=1 and 2 (E=6 MeV). It should be noted that the (a) and (b) diagrams express DD datasets, respectively, in a wide Z_c region and only in a deep Z_c region. In each of the (a) and (b) diagrams, the blue line expresses the doses of calculation, the set of gray marks expresses the doses copied from the W-K eMC dose datasets, the yellow line expresses the parallel-beam doses at infinite field, the brawn and blue marks express the doses of infinite field at Z_c = Z₂ and Z_c = Z₀(E), respectively (Figure 2). On the other hand, in each of the (c) and (d) diagrams, the solid lines express the OAD datasets of calculation, and the two sets of round marks express the OAD datasets copied from the W-K eMC dose datasets. It can be seen that the OAD datasets of calculation are reconstructed also by taking account of the balanced forms from shallow to deep depths and also by coinciding well with the W-K eMC dose datasets using Eqs. 1-4. It can be seen that much more accurate DD and OAD curves are yielded even at small Z_c regions, when compared with the results in Ref. [4] (this means that the function of Eq. 2 is reasonable).

• Supp. Fig. 4 shows the case of KK=3 and 4 (E=12 MeV) with the direct electron beams based on the standard eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 5 shows the case of KK=5 and 6 (E=18 MeV) with the direct electron beams based on the standard eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 6 shows the case of KK=7 & 8 (E=6 MeV) with the direct electron beams based on the TPS eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 7 shows the case of KK=9 & 10 (E=12 MeV) with the direct electron beams based on the TPS eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 8 shows the case of KK=11 & 12 (E=18 MeV) with the direct electron beams based on the TPS eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 9 shows the case of KK=13 & 14 (E=6 MeV) with the direct-plus-indirect electron beams based on the standard eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 10 shows the case of KK=15 & 16 (E=12 MeV) with the direct-plus-indirect electron beams based on the standard eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 11 shows the case of KK=17 & 18 (E=18 MeV) with the direct-plus-indirect electron beams based on the standard eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 12 shows the case of KK=19 & 20 (E=6 MeV) with the direct-plus-indirect electron beams based on the TPS eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 13 shows the case of KK=21 & 22 (E=12 MeV) with the direct-plus-indirect electron beams based on the TPS eMC. The others are the same as in Supp. Fig. 3.

• Supp. Fig. 14 shows the case of KK=23 & 24 (E=18 MeV) with the direct-plus-indirect electron beams based on the TPS eMC. The others are the same as in Supp. Fig. 3.

From the present investigation, the following features have been observed:
Dose differences between the DD curve of finite field and that of infinite field become greater as the increase of the beam energy (E). This means that the range of laterally scattered electrons becomes greater with the increase of the beam energy (E). This phenomenon can be explained by the 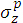or 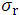function (Refs. 5 and 6).

The revised Gaussian-pencil-beam-model uses a mathematical σ_r expression, being reconstructed based on datasets of 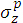for E=6,10,14,and 20 MeV as reported by Bruinvis et al. [5].

The three DD points of a₀ (E) for E=18 MeV in Figs. 8, 11, and 14 are respectively placed at a little wrong places. This fact has been found when writing this paper (we do not dare correct them in this paper).

The weak three points of the former papers of Refs. [3 and 4 regarding the calculated DD and OAD datasets, as noted in the introduction section, have been resolved.

ConclusionTop

To conclude this research report, we would like to conduct research on the development of the Gaussian pencil beam model when the phantom contains non-uniform materials and the beam entrance surface of the phantom is uneven.

Conflicts of interest
This study was carried out in collaboration with Technology of Radiotherapy Corporation, Tokyo, Japan. This sponsor had no control over the interpretation, writing, or publication of this work.

Supplementary dataTop

Supplementary Figures